Un corpo di massa 3 kg, inizialmente in quiete, si trova su una superficie orizzontale perfettamente liscia. Una forza orizzontale di intensità costante pari a 4,5 N agisce sul corpo per 20 s. Calcolare:
a) Qual è l’accelerazione acquisita dal corpo durante il tempo in cui la forza agisce?
b) Qual è la velocità del corpo quando la forza cessa di agire?
c) Qual è la distanza percorsa dal corpo fino a quando la forza cessa di agire?

Soluzione

Due corpi di masse m_a = 6 kg e m_b = 4 kg si trovano su una superficie orizzontale perfettamente liscia. Una forza orizzontale di intensità pari a 25 N viene applicata per spingere i due corpi. Calcolare l’accelerazione acquistata dall’insieme e l’intensità della forza di contatto tra i corpi.

Soluzione

Due blocchi, di masse m_a = 0,35 kg e m_b = 1,15 kg, si trovano su una superficie orizzontale perfettamente liscia, i blocchi sono collegati da una fune ideale. Una forza orizzontale di intensità costante pari a 15 N viene applicata trascinando i due blocchi. Calcolare l’accelerazione acquisita dal sistema e la tensione nella fune che collega i blocchi.

Soluzione

Un uomo di massa m = 70 kg si trova in un ascensore, il quale si muove con accelerazione a = 2 m/s². Determinare:
a) La forza con cui l’uomo agisce sul pavimento dell’ascensore, se l’ascensore sta scendendo;
b) La forza con cui l’uomo agisce sul pavimento dell’ascensore, se l’ascensore sta salendo;
c) Per quale accelerazione dell’ascensore la forza dell’uomo sul pavimento dell’ascensore sarà uguale a zero?

Soluzione

Una locomotiva di 130 tonnellate traina un vagone di 120 tonnellate. La forza massima che il gancio di trazione locomotiva-vagone può sopportare è di 2.900 kN. Determinare la massima forza motrice che la locomotiva può esercitare per non rompere il gancio. Trascurare le forze di resistenza.

Soluzione

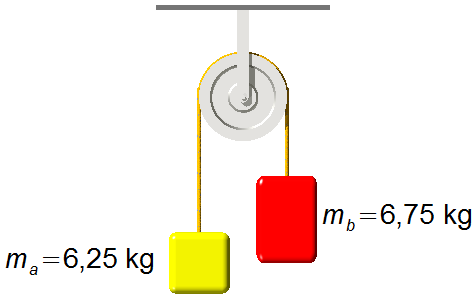
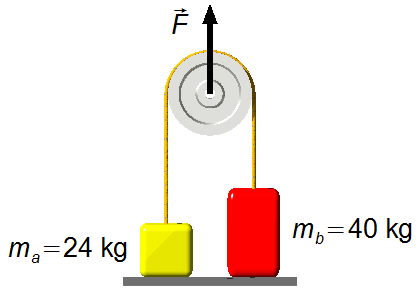
Una macchina di Atwood possiede masse m_a = 6,25 kg e m_b = 6,75 kg, collegate da una fune ideale, inestensibile e di massa trascurabile, tramite una carrucola anch’essa ideale. Determinare:
a) L’accelerazione del sistema;
b) La tensione nella fune che collega le masse;
c) La tensione nella fune che sostiene il sistema al soffitto.

Soluzione

Nel sistema della figura, il corpo A scivola su un piano orizzontale senza attrito, trascinato da B che scende verticalmente. I corpi A e B sono collegati tra loro da una corda inestensibile di massa trascurabile parallela al piano che passa attraverso la puleggia di massa trascurabile senza attrito. Le masse di A e B valgono rispettivamente 32 kg e 8 kg. Determinare l’accelerazione del sistema e l’intensità della forza di tensione nella corda.

Soluzione

Nel sistema della figura, il corpo B scivola su un piano orizzontale senza attrito, esso è collegato da un sistema di corde e carrucole ideali a due corpi A e C che si muovono verticalmente. Le masse di A, B e C valgono rispettivamente 5 kg, 2 kg e 3 kg. Determinare l’accelerazione del sistema e l’intensità delle forze di tensione nelle corde.

Soluzione

In una macchina di Atwood i due corpi, appoggiati su una superficie orizzontale, sono collegati da una fune, di massa trascurabile e inestensibile, che passa attraverso una carrucola, priva di inerzia e di attrito. Date le masse m_a = 24 kg e m_b = 40 kg. Determinare le accelerazioni dei corpi quando:
a) F = 400 N;
b) F = 720 N;
c) F = 1200 N.

Soluzione