Grundbegriffe
Ein Körper mit einer Masse von 3 kg befindet sich zunächst in Ruhe auf einer vollkommen glatten
horizontalen Oberfläche. Eine konstante horizontale Kraft von 4,5 N wirkt 20 s lang auf den Körper ein.
Berechne:
a) Welche Beschleunigung erfährt der Körper während der Einwirkzeit der Kraft?
b) Welche Geschwindigkeit hat der Körper, wenn die Kraft nicht mehr wirkt?
c) Welche Strecke legt der Körper zurück, bis die Kraft nicht mehr wirkt?

Ein Mann mit der Masse m = 70 kg befindet sich in einem Aufzug, der sich mit einer Beschleunigung
a = 2 m/s2 bewegt. Bestimme:
a) Die Kraft, mit der der Mann auf den Boden des Aufzugs wirkt, wenn der Aufzug nach unten fährt;
b) Die Kraft, mit der der Mann auf den Boden des Aufzugs wirkt, wenn der Aufzug nach oben fährt;
c) Für welche Beschleunigung des Aufzugs die Kraft des Mannes auf den Boden des Aufzugs null ist?
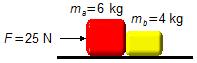
Eine Lokomotive mit 130 Tonnen zieht einen Waggon mit 120 Tonnen. Die maximale Kraft, die die Kupplung zwischen Lokomotive und Waggon aushält, beträgt 2.900 kN. Bestimmen Sie die maximale Antriebskraft, die die Lokomotive ausüben kann, ohne dass die Kupplung reißt. Widerstandskräfte werden vernachlässigt.
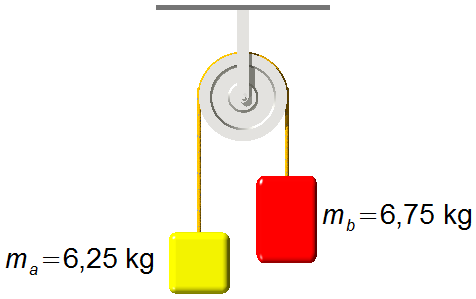
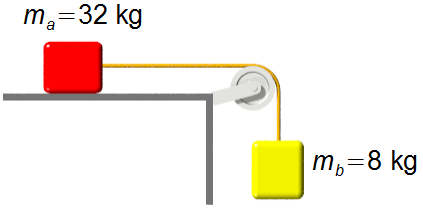
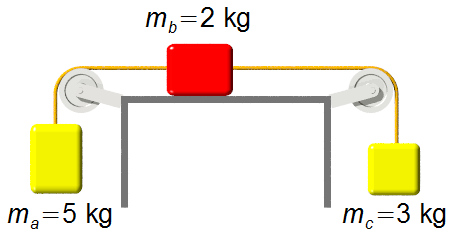
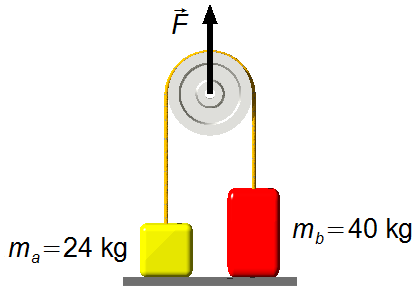
Atwoodsche Fallmaschine
a) Die Beschleunigung des Systems;
b) Die Zugkraft zwischen den Massen;
c) Die Zugkraft im Seil, das das System an der Decke hält.
a) F = 400 N;
b) F = 720 N;
c) F = 1200 N.

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .