Gelöste Übung zur Dynamik

Zwei Körper mit den Massen m_a = 6 kg und m_b = 4 kg befinden sich auf einer vollkommen glatten horizontalen Oberfläche. Eine horizontale Kraft von 25 N wird auf das System ausgeübt, um beide Körper zu schieben. Berechne die vom System erreichte Beschleunigung; und die Betrag der Kontaktkraft zwischen den Körpern.

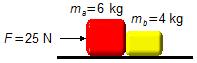
Gegebene Daten:

Masse des Körpers A: m_a = 6 kg;
Masse des Körpers B: m_b = 4 kg;
Auf das System ausgeübte Kraft: F = 25 N.

Schema des Problems:

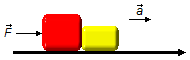
Wir wählen ein nach rechts orientiertes Bezugssystem, in dieselbe Richtung wie die aufgebrachte Kraft \( \vec F \). Diese Kraft bewirkt eine Beschleunigung a des Systems.

Abb. 1

Durch das Zeichnen eines Freikörperdiagramms erhalten wir die auf die Blöcke wirkenden Kräfte.

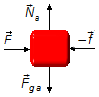
Körper A:
- Horizontale Richtung:
  - \( \vec F \) : auf den Körper wirkende äußere Kraft;
  - \( -\vec f \) : Reaktionskraft von Körper B auf A.
- Vertikale Richtung:
  - \( {\vec N}_a \) : Normalkraft der Oberfläche auf den Körper;
  - \( {\vec P}_{ga} \) : Gewichtskraft des Körpers A.

Abb. 2

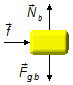
Körper B:
- Horizontale Richtung:
  - \( \vec f \): Aktionskraft von Körper A auf B.
- Vertikale Richtung:
  - \( {\vec N}_b \): Normalkraft der Oberfläche auf den Körper;
  - \( {\vec P}_{gb} \): Gewichtskraft des Körpers B.

Abb. 3

Lösung:

Anwendung des 2. Newtonschen Gesetzes

\[ \begin{gather} \bbox[#99CCFF,10px] {\vec F=m\vec a} \end{gather} \]

Körper A:

In vertikaler Richtung erfolgt keine Bewegung, die Normalkraft und die Gewichtskraft heben sich gegenseitig auf.
In horizontaler Richtung gilt

\[ \begin{gather} F-f=m_aa \tag{I} \end{gather} \]

Körper B:

In vertikaler Richtung erfolgt keine Bewegung, die Normalkraft und die Gewichtskraft heben sich gegenseitig auf.
In horizontaler Richtung gilt

\[ \begin{gather} {f=m_ba} \tag{II} \end{gather} \]

Die Gleichungen (I) und (II) bilden ein lineares Gleichungssystem mit zwei Unbekannten (f und a)

\[ \begin{gather} \left\{ \begin{array}{rr} F-f&=m_aa \\ f&=m_ba \end{array} \right. \end{gather} \]

Einsetzen der Gleichung (II) in die Gleichung (I), wir erhalten die Beschleunigung.

\[ \begin{gather} F-m_ba=m_aa \\[5pt] F=a(m_a+m_b) \\[5pt] a=\frac{F}{m_a+m_b} \\[5pt] a=\frac{25}{6+4} \\[5pt] a=\frac{25}{10} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {a=2,5\;\mathrm{m/s^2}} \end{gather} \]

Anmerkung: Da beide Körper gemeinsam durch eine einzige Kraft beschleunigt werden, besitzen sie dieselbe Beschleunigung. Das System verhält sich, als wäre es ein einzelner Körper, dessen Gesamtmasse sich aus der Summe der Massen beider Körper ergibt, A e B.

Einsetzen der oben ermittelten Beschleunigung in die Gleichung (II), wir erhalten die Kontaktkraft zwischen den Körpern

\[ \begin{gather} f=4\times 2,5 \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {f=10\;\mathrm N} \end{gather} \]

Anmerkung: Alternativ könnten wir die Beschleunigung in die Gleichung (I) einsetzen, um die Kontaktkraft zu erhalten. In diesem Fall hätten wir

\[ \begin{gather} 25-f=6\times 2,5\Rightarrow 25-f=15\Rightarrow f=10\;\mathrm N \end{gather} \]

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .