Solved Problem on Dynamics

Two bodies of masses m_a = 6 kg and m_b = 4 kg are on a frictionless horizontal surface. A horizontal force of constant magnitude equal to 25 N is applied to push the two bodies. Find the acceleration acquired by the set and the magnitude of the contact force between the bodies.

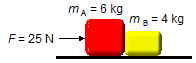
Problem data:

Mass of body A: m_a = 6 kg;
Mass of body B: m_b = 4 kg;
Force applied to the system: F = 25 N.

Problem diagram:

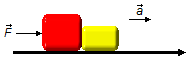
We choose a frame of reference oriented to the right in the same direction as the applied force \( \vec F \) and produce an acceleration a on the system.

Figure 1

Drawing a Free-Body Diagram for each body

Body A:
- Horizontal direction:
  - \( \vec F \) : force applied to the body;
  - \( -\vec f \) : reaction force of body B on A.
- Vertical direction:
  - \( {\vec N}_a \) : normal reaction force of the surface on the body;
  - \( {\vec W}_a \) : weight of body A.

Figure 2

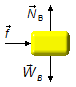
Body B:
- Horizontal direction:
  - \( \vec f \): action force of body A on B.
- Vertical direction:
  - \( {\vec N}_b \): normal reaction force of the surface on the body;
  - \( {\vec W}_b \): weight of body B.

Figure 3

Solution:

Applying Newton's Second Law

\[ \begin{gather} \bbox[#99CCFF,10px] {\vec F=m\vec a} \end{gather} \]

Body A:

In the vertical direction, there is no motion, the normal force and weight cancel each other out.
In the horizontal direction

\[ \begin{gather} F-f=m_aa \tag{I} \end{gather} \]

Body B:

In the vertical direction, there is no motion, the normal force and weight cancel each other out.
In the horizontal direction

\[ \begin{gather} {f=m_ba} \tag{II} \end{gather} \]

Equations (I) and (II) can be written as a system of linear equations with two variables (f and a)

\[ \begin{gather} \left\{ \begin{array}{rr} F-f&=m_aa \\ f&=m_ba \end{array} \right. \end{gather} \]

substituting equation (II) into equation (I), we have the acceleration

\[ \begin{gather} F-m_ba=m_aa \\[5pt] F=a(m_a+m_b) \\[5pt] a=\frac{F}{m_a+m_b} \\[5pt] a=\frac{25\;\mathrm N}{(6\;\mathrm kg)+(4\;\mathrm kg)}\\[5pt] a=\frac{25\;\mathrm{\frac{\cancel{kg}.m}{s^2}}}{10\;\mathrm{\cancel{kg}}} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {a=2.5\;\mathrm{m/s^2}} \end{gather} \]

Note: Since the two bodies form a set subjected to the same force, both have the same acceleration. The system behaves as if it were a single body with total mass given by the sum of the masses of the two bodies, A and B.

Substituting the acceleration found in equation (II), we have the force of contact between the bodies

\[ \begin{gather} f=(4\;\mathrm{kg})\left(2.5\;\mathrm{\frac{m}{s^2}}\right) \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {f=10\;\mathrm N} \end{gather} \]

Note: In the same way, we could substitute the acceleration in the equation (I) to obtain the contact force

\[ \begin{gather} (25\;\mathrm N)-f=(6\;\mathrm{kg})\left(2.5\;\mathrm{\frac{m}{s^2}}\right)\Rightarrow (25\;\mathrm N)-f=15\;\mathrm N\Rightarrow f=10\;\mathrm N \end{gather} \]

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .