Gelöste Übung zur Dynamik
Werbung   

Eine Lokomotive mit 130 Tonnen zieht einen Waggon mit 120 Tonnen. Die maximale Kraft, die die Kupplung zwischen Lokomotive und Waggon aushält, beträgt 2.900 kN. Bestimmen Sie die maximale Antriebskraft, die die Lokomotive ausüben kann, ohne dass die Kupplung reißt. Widerstandskräfte werden vernachlässigt.

 

Gegebene Daten:

  • Masse der Lokomotive:    mL = 130 t = 130.000 kg;
  • Masse des Waggons:    mW = 120 t = 120.000 kg;
  • Maximal ertragbare Kupplungskraft:    T = 2.900 kN = 2.900.000 N.

Schema des Problems:

Das System kann durch zwei Blöcke dargestellt werden, welche Lokomotive und Waggon repräsentieren, verbunden durch ein Seil, das die Kupplung zwischen beiden darstellt (Abbildung 1).

Abb. 1
Wir wählen ein Bezugssystem, das nach rechts in Richtung der angreifenden Kraft \( {\vec F}_{\small M} \) orientiert ist. Diese erzeugt eine Beschleunigung \( \vec a \) des Systems.
Abb. 2

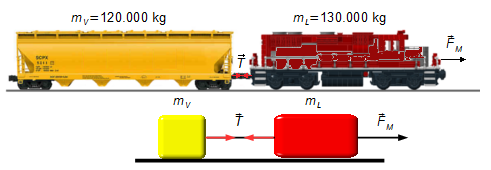
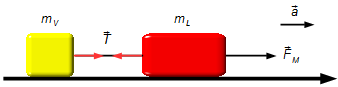
Durch das Zeichnen eines Freikörperdiagramms erhalten wir die auf die Blöcke wirkenden Kräfte.

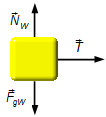
  • Waggon (Abbildung 3):
    • Horizontale Richtung:
      • \( \vec T \): Zugkraft in der Kupplung.
    • Vertikale Richtung:
      • \( {\vec N}_{\small W} \): Normalkraft der Oberfläche auf den Waggon;
      • \( {\vec F}_{g\small W} \): Gewichtskraft des Waggons.
Abb. 3
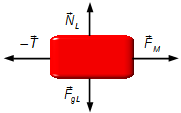
  • Lokomotive (Abbildung 4):
    • Horizontale Richtung:
      • \( {\vec F}_{\small M} \): Antriebskraft der Lokomotive;
      • \( -\vec T \): Zugkraft in der Kupplung.
    • Vertikale Richtung:
      • \( {\vec N}_{\small L} \): Normalkraft der Oberfläche auf die Lokomotive;
      • \( {\vec F}_{g\small L} \): Gewichtskraft der Lokomotive.
Abb. 4

Lösung:

Anwendung des 2. Newtonschen Gesetzes

\[ \begin{gather} \bbox[#99CCFF,10px] {\vec F=m\vec a} \tag{I} \end{gather} \]
  • Für den Waggon:

In vertikaler Richtung erfolgt keine Bewegung, die Normalkraft und die Gewichtskraft heben einander auf.
In horizontaler Richtung

\[ \begin{gather} T=m_{\small W}a \tag{II} \end{gather} \]
  • Für die Lokomotive:

In vertikaler Richtung erfolgt keine Bewegung, die Normalkraft und die Gewichtskraft heben einander auf.
In horizontaler Richtung

\[ \begin{gather} F_{\small M}-T=m_{\small L}a \tag{III} \end{gather} \]

Die Gleichungen (II) und (III) bilden ein lineares Gleichungssystem mit zwei Unbekannten (FM und a)

\[ \begin{gather} \left\{ \begin{array}{r} T=m_{\small W}a\\ F_{\small M}-T=m_{\small L}a \end{array} \right. \end{gather} \]

aus der ersten Gleichung des Systems isolieren wir die Beschleunigung a

\[ \begin{gather} a=\frac{T}{m_{\small W}} \end{gather} \]

Einsetzen der Beschleunigung in die zweite Gleichung des Systems

\[ \begin{gather} F_{\small M}-T=m_{\small L}\frac{T}{m_{\small W}} \end{gather} \]
\[ \begin{gather} F_{\small M}=T+m_{\small L}\frac{T}{m_{\small W}} \\[5pt] F_{\small M}=2900000+130000\times \frac{2900000}{120000} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {F_{\small M}=6.041.666\;\mathrm N} \end{gather} \]
Anmerkung: Man sieht, dass die gefundene Beschleunigung für einen Zug unrealistisch ist
\[ \begin{gather} a=\frac{T}{m_{\small W}} \\[5pt] a=\frac{2.900.000}{120.000} \\[5pt] a=24,2\;\mathrm{m/s^2} \end{gather} \]
er würde von 0 auf 100 km/h in etwa 1 Sekunde beschleunigen. Eine Zugkupplung ist jedoch sehr widerstandsfähig und muss einer sehr großen Kraft ausgesetzt werden, um zu brechen.
Werbung   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .