Esercizio Risolto di Dinamica
pubblicità   

Una locomotiva di 130 tonnellate traina un vagone di 120 tonnellate. La forza massima che il gancio di trazione locomotiva-vagone può sopportare è di 2.900 kN. Determinare la massima forza motrice che la locomotiva può esercitare per non rompere il gancio. Trascurare le forze di resistenza.

 

Dati del problema:

  • Massa della locomotiva:    mL = 130 t = 130.000 kg;
  • Massa del vagone:    mV = 120 t = 120.000 kg;
  • Forza massima sopportata dal gancio:    T = 2.900 kN = 2.900.000 N.

Schema del problema:

Il sistema può essere rappresentato da due blocchi, che rappresentano la locomotiva e il vagone, collegati da una corda che rappresenta il gancio tra i due (Figura 1).

Figura 1
Scegliamo un sistema di riferimento orientato verso destra, nello stesso senso della forza \( {\vec F}_{\small M} \) applicata che produce l’accelerazione \( \vec a \) del sistema.
Figura 2

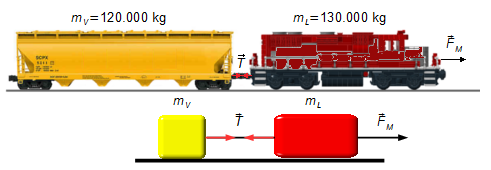
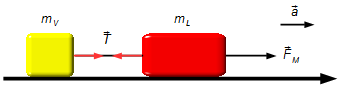
Facendo un Diagramma del Corpo Libero, abbiamo le forze che agiscono sui corpi.

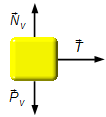
  • Vagone (Figura 3):
    • Direzione orizzontale:
      • \( \vec T \): forza di trazione nel gancio.
    • Direzione verticale:
      • \( {\vec N}_{\small V} \): forza normale di reazione della superficie sul vagone;
      • \( {\vec P}_{\small V} \): forza peso del vagone.
Figura 3
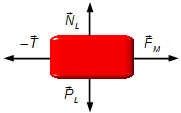
  • Locomotiva (Figura 4):
    • Direzione orizzontale:
      • \( {\vec F}_{\small M} \): forza motrice esercitata dalla locomotiva;
      • \( -\vec T \): forza di trazione nel gancio.
    • Direzione verticale:
      • \( {\vec N}_{\small L} \): orza normale di reazione della superficie sulla locomotiva;
      • \( {\vec P}_{\small L} \): orza peso della locomotiva.
Figura 4

Soluzione:

Applicando la Seconda Legge di Newton

\[ \begin{gather} \bbox[#99CCFF,10px] {\vec F=m\vec a} \tag{I} \end{gather} \]
  • Per il vagone:

Nella direzione verticale, non c’è movimento, la forza normale e la forza peso si annullano.
Nella direzione orizzontale

\[ \begin{gather} T=m_{\small V}a \tag{II} \end{gather} \]
  • Per la locomotiva:

Nella direzione verticale, non c’è movimento, la forza normale e la forza peso si annullano.
Nella direzione orizzontale

\[ \begin{gather} F_{\small M}-T=m_{\small L}a \tag{III} \end{gather} \]

Le equazioni (II) e (III) formano un sistema di due equazioni a due incognite (FM e a)

\[ \begin{gather} \left\{ \begin{array}{r} T=m_{\small V}a\\ F_{\small M}-T=m_{\small L}a \end{array} \right. \end{gather} \]

dalla prima equazione del sistema isoliamo l’accelerazione a

\[ \begin{gather} a=\frac{T}{m_{\small V}} \end{gather} \]

sostituendo l’accelerazione nella seconda equazione del sistema

\[ \begin{gather} F_{\small M}-T=m_{\small L}\frac{T}{m_{\small V}} \end{gather} \]
\[ \begin{gather} F_{\small M}=T+m_{\small L}\frac{T}{m_{\small V}} \\[5pt] F_{\small M}=2900000+130000\times \frac{2900000}{120000} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {F_{\small M}=6.041.666\;\mathrm N} \end{gather} \]
Osservazione: Si vede che l’accelerazione trovata è impensabile per un treno
\[ \begin{gather} a=\frac{T}{m_{\small V}} \\[5pt] a=\frac{2.900.000}{120.000} \\[5pt] a=24,2\;\mathrm{m/s^2} \end{gather} \]
esso accelererebbe da 0 a 100 km/h in circa 1 secondo. Il gancio di un treno è piuttosto resistente e deve essere sottoposto a una forza molto grande per rompersi.
pubblicità   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .