Eine Atwoodsche Maschine besteht aus den Massen m_a = 6,25 kg und m_b = 6,75 kg, die durch ein ideales, undehnbares und masseloses Seil verbunden sind, das über eine ebenfalls ideale Rolle läuft. Bestimmen Sie:
a) Die Beschleunigung des Systems;
b) Die Zugkraft zwischen den Massen;
c) Die Zugkraft im Seil, das das System an der Decke hält.

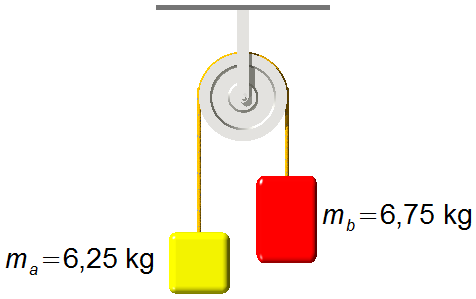
Gegebene Daten:

• Masse des Körpers A:    m_a = 6,25 kg;
• Masse des Körpers B:    m_b = 6,75 kg;
• Erdbeschleunigung:    g = 9,8 m/s².

Schema des Problems:

Da die Masse des Körpers B größer ist als die Masse des Körpers A, bewegt sich Block B nach unten, während Block A nach oben steigt. Das System ist ideal, daher ist die Beschleunigung für das gesamte System gleich.
Wir wählen ein Bezugssystem mit positiver Orientierung in Richtung der Abwärtsbewegung von Block B, also in Richtung der Erdbeschleunigung.
Da das Seil ideal ist (masselos und undehnbar), überträgt es lediglich die Gewichtskräfte der Blöcke (Abbildung 1).

Abb. 1

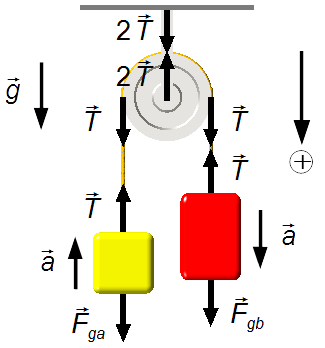
Durch das Zeichnen eines Freikörperdiagramms erhalten wir die auf die Blöcke wirkenden Kräfte.

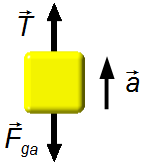
• Körper A (Abbildung 2):
  • \( \vec T \) : Zugkraft;
  • \( {\vec F}_{ga} \) : Gewichtskraft des Körpers A.

Abb. 2

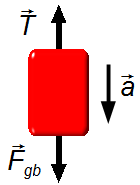
• Körper B (Abbildung 3):
  • \( \vec T \) : Zugkraft;
  • \( {\vec F}_{gb} \) : Gewichtskraft des Körpers B.

Abb. 3

Lösung:

a) Anwendung des 2. Newtonschen Gesetzes

• Körper A:

• Körper B:

Die Gewichtskraft ist gegeben durch

für die Körper A und B

Einsetzen von Gleichung (III-a) in Gleichung (I)

Einsetzen von Gleichung (III-b) in Gleichung (II)

Die Gleichungen (IV) und (V) bilden ein lineares Gleichungssystem mit zwei Unbekannten (a und T). Addieren wir die beiden Gleichungen

b) Durch Einsetzen des in Teil (a) gefundenen Wertes in die erste (oder zweite) Gleichung des Systems erhalten wir die Zugkraft

c) Da die Rolle die Seilkraft auf beide Seiten gleichmäßig überträgt, beträgt die Seilkraft im Seil, das das System an der Decke hält, das Doppelte (Abbildung 1):