Una macchina di Atwood possiede masse m_a = 6,25 kg e m_b = 6,75 kg, collegate da una fune ideale, inestensibile e di massa trascurabile, tramite una carrucola anch’essa ideale. Determinare:
a) L’accelerazione del sistema;
b) La tensione nella fune che collega le masse;
c) La tensione nella fune che sostiene il sistema al soffitto.

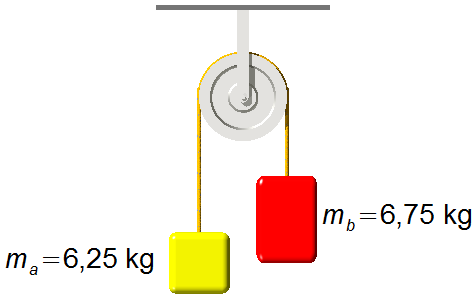
Dati del problema:

• Massa del corpo A:    m_a = 6,25 kg;
• Massa del corpo B:    m_b = 6,75 kg;
• Accelerazione di gravità:    g = 9,8 m/s².

Schema del problema:

Poiché la massa del blocco B è maggiore della massa del blocco A, il blocco B scende mentre il blocco A sale. Il sistema è ideale, pertanto, l’accelerazione è la stessa per tutto l’insieme.
Scegliamo un sistema di riferimento orientato positivamente nel senso di discesa del blocco B, stesso senso dell’accelerazione di gravità.
Poiché la fune è ideale (di massa trascurabile e inestensibile) essa trasmette soltanto la forza di tensione dei blocchi (Figura 1).

Figura 1

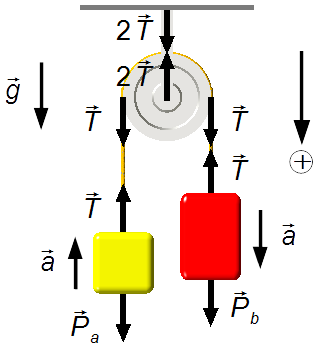
Facendo un Diagramma del Corpo Libero, abbiamo le forze che agiscono sui blocchi.

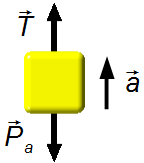
• Corpo A (Figura 2):
  • \( \vec T \) : forza di tensione nella fune;
  • \( {\vec P}_a \) : forza peso del blocco A.

Figura 2

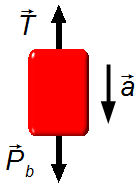
• Corpo B (Figura 3):
  • \( \vec T \) : forza di tensione nella fune;
  • \( {\vec P}_b \) : forza peso del blocco B.

Figura 3

Soluzione:

a) Applicando la Seconda Legge di Newton

• Corpo A:

• Corpo B:

La forza peso è data da

per i corpi A e B

sostituendo l’equazione (III-a) nell’equazione (I)

sostituendo l’equazione (III-b) nell’equazione (II)

Le equazioni (IV) e (V) formano un sistema di due equazioni a due incognite (a e T). Sommando le due equazioni

b) Sostituendo il valore dell’accelerazione trovato nell’item (a) nella prima (o nella seconda equazione del sistema), otteniamo la tensione nella fune

c) Poiché la carrucola distribuisce la tensione ugualmente nella fune da entrambi i lati, la tensione nella fune che sostiene il sistema al soffitto sarà il doppio (Figura 1)