Gelöste Übung zur Dynamik
Werbung   

Ein Mann mit der Masse m = 70 kg befindet sich in einem Aufzug, der sich mit einer Beschleunigung a = 2 m/s2 bewegt. Bestimme:
a) Die Kraft, mit der der Mann auf den Boden des Aufzugs wirkt, wenn der Aufzug nach unten fährt;
b) Die Kraft, mit der der Mann auf den Boden des Aufzugs wirkt, wenn der Aufzug nach oben fährt;
c) Für welche Beschleunigung des Aufzugs die Kraft des Mannes auf den Boden des Aufzugs null ist?

 

Gegebene Daten:

  • Masse des Mannes:    m = 70 kg;
  • Beschleunigung des Aufzugs:    a = 2 m/s2;
  • Erdbeschleunigung:    g = 9,8 m/s2.

Lösung:

a) Wir wählen ein Bezugssystem in Richtung der Aufzugsbeschleunigung nach unten als positiv.
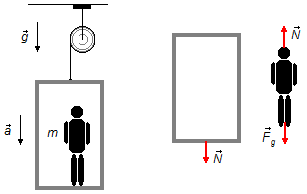
Durch das Zeichnen eines Freikörperdiagramms erhalten wir die auf die Körper wirkenden Kräfte (Abbildung 1).

  • Aufzug:
    • \( \vec N \): kraft, mit der der Mann auf den Boden des Aufzugs wirkt.
  • Mann:
    • \( {\vec F}_g \): Gewichtskraft des Mannes.
    • \( \vec N \): Normalkraft – Reaktionskraft des Aufzugsbodens auf den Mann.
Abb. 1
Anmerkung: Auch der Aufzug hat eine Gewichtskraft. Aber da wir die Kraft finden wollen, die der Mann auf den Aufzug ausübt, und diese in ihrem Betrag gleich der Reaktion des Aufzugs auf den Mann ist, also \( \vec N \), man muss nur die Kräfte analysieren, die auf den Mann wirken.

Anwendung des 2. Newtonschen Gesetzes

\[ \begin{gather} \bbox[#99CCFF,10px] {\vec F=m\vec a} \end{gather} \]
  • Mann:
\[ \begin{gather} F_g-N=ma \tag{I} \end{gather} \]

die Gewichtskraft ist gegeben durch

\[ \begin{gather} \bbox[#99CCFF,10px] {F_g=mg} \end{gather} \]

Einsetzen dieser Gleichung in die Gleichung (I)

\[ \begin{gather} mg-N=ma \\[5pt] N=m\;(g-a) \tag{II} \\[5pt] N=70\times(9,8-2) \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {N=546\;\mathrm N} \end{gather} \]

 

b) Wir wählen ein Bezugssystem in Richtung der Aufzugsbeschleunigung nach oben als positiv.
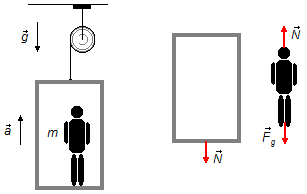
Erneut zeichnen wir ein Freikörperdiagramm (Abbildung 2) und wenden das 2. Newtonsche Gesetz an.
Die auf den Aufzug und auf den Mann wirkenden Kräfte sind dieselben wie in Teil (a) (Abbildungen 1 und 2).

Abb. 2

Wir wenden Gleichung (I) erneut auf den Mann an, berücksichtigen aber jetzt die umgekehrte Richtung der Beschleunigung des Aufzugs

\[ \begin{gather} N-mg=ma \\[5pt] N=m\;(g+a) \tag{III} \\[5pt] N=70\times(9,8+2) \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {N=826\;\mathrm N} \end{gather} \]

 

c) Wenn der Mann keine Kraft auf den Boden des Aufzugs ausübt, muss die Normalkraft null sein, also N = 0. Diese Bedingung setzen wir in Gleichung (II) aus Teil (a) ein

\[ \begin{gather} 0=m\;(g-a) \\[5pt] g-a=\frac{0}{m} \\[5pt] g-a=0 \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {a=g=9,8\;\mathrm{m/s^2}} \end{gather} \]
Anmerkung 1: Dieses Ergebnis bedeutet, dass sich der Aufzug und der Mann im freien Fall befinden. Der Mann "löst" sich vom Boden des Aufzugs; es gibt keine Aktion des Mannes auf den Aufzug und keine Reaktion des Aufzugs auf den Mann.

Anmerkung 2: Wenn wir anstelle von Gleichung (II) aus Teil (a) die Gleichung (III) aus Teil (b) verwendet hätten, mit der Bedingung N = 0, hätten wir a = −g erhalten. Das bedeutet, dass der Betrag der Beschleunigung derselbe wäre, aber ihre Richtung – im Teil (b) nach oben – müsste nach unten geändert werden, was mit der Situation in Teil (a) übereinstimmt.
Werbung   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .