Esercizio Risolto di Dinamica

Un uomo di massa m = 70 kg si trova in un ascensore, il quale si muove con accelerazione a = 2 m/s². Determinare:
a) La forza con cui l’uomo agisce sul pavimento dell’ascensore, se l’ascensore sta scendendo;
b) La forza con cui l’uomo agisce sul pavimento dell’ascensore, se l’ascensore sta salendo;
c) Per quale accelerazione dell’ascensore la forza dell’uomo sul pavimento dell’ascensore sarà uguale a zero?

Dati del problema:

Massa dell’uomo: m = 70 kg;
Accelerazione dell’ascensore: a = 2 m/s²;
Accelerazione di gravità: g = 9,8 m/s².

Soluzione:

a) Scegliamo un sistema di riferimento orientato verso il basso, nello stesso senso dell’accelerazione dell’ascensore.
Facendo un Diagramma del Corpo Libero, abbiamo le forze che agiscono sui corpi (Figura 1).

Ascensore:
- \( \vec N \): azione dell’uomo sul pavimento dell’ascensore.

Uomo::
- \( \vec P \): forza peso dell’uomo.
- \( \vec N \): forza di reazione del pavimento dell’ascensore sull’uomo.

Figura 1

Osservazione: Nell’ascensore esiste anche il peso proprio dell’ascensore. Ma poiché vogliamo determinare la forza che l’uomo esercita sull’ascensore e questa è uguale, in modulo, alla reazione dell’ascensore sull’uomo, \( \vec N \), basta analizzare le forze che agiscono sull’uomo.

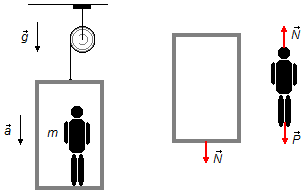
Applicando la Seconda Legge di Newton

\[ \begin{gather} \bbox[#99CCFF,10px] {\vec F=m\vec a} \end{gather} \]

Uomo:

\[ \begin{gather} P-N=ma \tag{I} \end{gather} \]

la forza peso è data da

\[ \begin{gather} \bbox[#99CCFF,10px] {P=mg} \end{gather} \]

sostituendo questa equazione nell'equazione (I)

\[ \begin{gather} mg-N=ma \\[5pt] N=m\;(g-a) \tag{II} \\[5pt] N=70\times(9,8-2) \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {N=546\;\mathrm N} \end{gather} \]

b) Scegliamo un sistema di riferimento orientato verso l’alto, nello stesso senso dell’accelerazione dell’ascensore.
Ancora una volta, facendo un Diagramma del Corpo Libero, abbiamo le forze che agiscono sui corpi (Figura 2) e possiamo applicare la Seconda Legge di Newton.
Le forze che agiscono sull’ascensore e sull’uomo sono le stesse del punto (a), (Figure 1 e 2).

Figura 2

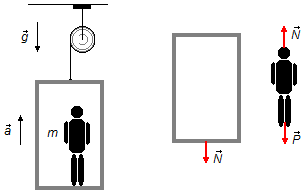
Applicando l’equazione (I) all’uomo, considerando ora l’inversione nel senso dell’accelerazione dell’ascensore

\[ \begin{gather} N-mg=ma \\[5pt] N=m\;(g+a) \tag{III} \\[5pt] N=70\times(9,8+2) \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {N=826\;\mathrm N} \end{gather} \]

c) Se l’uomo non esercita forza sul pavimento dell’ascensore, dobbiamo avere la forza normale nulla, N = 0. Sostituendo questa condizione nell’equazione (II) del punto (a)

\[ \begin{gather} 0=m\;(g-a) \\[5pt] g-a=\frac{0}{m} \\[5pt] g-a=0 \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {a=g=9,8\;\mathrm{m/s^2}} \end{gather} \]

Osservazione 1: Questo risultato significa che l’ascensore e l’uomo sono in caduta libera. L’uomo tende a “staccarsi” dal pavimento dell’ascensore, non c’è azione dell’uomo sull’ascensore e non c’è reazione dell’ascensore sull’uomo.

Osservazione 2: Se invece di usare l’equazione (II) del punto (a), avessimo usato l’equazione (III) del punto (b), con la condizione N = 0, il risultato sarebbe a = −g. Ciò significa che il modulo dell’accelerazione sarebbe lo stesso, ma il senso dell’accelerazione, che nel punto (b) è orientato verso l’alto, dovrebbe essere invertito verso il basso, il che coincide con la situazione del punto (a).

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .