Solved Problem on Dynamics

A man of mass m = 70 kg, is in an elevator, this one moves with acceleration a = 2 m/s². Determine:
a) The force of the man on the floor of the elevator, if the elevator is accelerating downwards;
b) The force of the man on the floor of the elevator, if the elevator is accelerating upwards;
c) For what acceleration of the elevator will the force of the man on the floor be equal to zero?

Problem data:

Mass of the man: m = 70 kg;
Acceleration of the elevator: a = 2 m/s²;
Acceleration due to gravity: g = 9.8 m/s².

Solution:

a) We choose a reference frame oriented in the downward direction of the elevator, the same direction of the acceleration.
Drawing a Free-Body Diagram for the elevator and the man (Figure 1).

Elevator:
- \( \vec N \): action of the man on the floor of the elevator.

Mam:
- \( \vec W \): weight of the man;
- \( \vec N \): normal reaction force of the elevator on the man.

Figure 1

Note: In the elevator, there is also the weight of the elevator itself. Since we want to find the force that man exerts on the elevator, which is equal in magnitude to the normal force of the elevator on the man, \( \vec N \), it is sufficient to analyze the forces acting on the man.

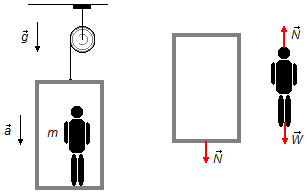
Applying Newton's Second Law

\[ \begin{gather} \bbox[#99CCFF,10px] {\vec F=m\vec a} \end{gather} \]

Man:

\[ \begin{gather} W-N=ma \tag{I} \end{gather} \]

the weight is given by

\[ \begin{gather} \bbox[#99CCFF,10px] {W=mg} \end{gather} \]

substituting this equation into equation (I)

\[ \begin{gather} mg-N=ma \\[5pt] N=m\;(g-a) \tag{II} \\[5pt] N=\left(70\;\mathrm{kg}\right)\left(9.8\;\mathrm{m/s^2}-2\;\mathrm{m/s^2}\right) \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {N=546\;\mathrm N} \end{gather} \]

b) We choose a reference frame oriented in the upward direction of the elevator, the same direction of the acceleration.
Drawing a Free-Body Diagram again, we have the forces that act on the bodies (Figure 2), and we can apply Newton's Second Law.
The forces acting on the elevator and the man are the same as in item (a) (Figures 1 and 2).

Figure 2

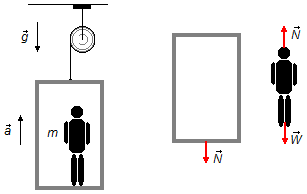
Using the equation (I) for the man, with the inversion in the direction of the acceleration of the elevator

\[ \begin{gather} N-mg=ma \\[5pt] N=m\;(g+a) \tag{III} \\[5pt] N=\left(70\;\mathrm{kg}\right)\left(9.8\;\mathrm{m/s^2}+2\;\mathrm{m/s^2}\right) \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {N=826\;\mathrm N} \end{gather} \]

c) If the man does not exert force on the floor of the elevator, we have the normal force is zero, N = 0. Substituting this condition in the equation (II) of item (a)

\[ \begin{gather} 0=m\;(g-a) \\[5pt] g-a=\frac{0}{m} \\[5pt] g-a=0 \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {a=g=9.8\;\mathrm{m/s^2}} \end{gather} \]

Note 1: This result means that the elevator and the man are in free fall. The man tends to "take off" from the elevator floor, and there is no action of the man on the elevator, therefore there is no reaction force on the man due to the elevator.

Note 2: If instead of using the equation (II) of item (a), we had used the equation (III) of item (b), with the condition of N = 0, the result would be a = −g. This means that the magnitude of the acceleration is the same, but the direction of the acceleration, which in item (b) is upwards, would have to be downwards, coinciding with the situation of item (a).

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .