Gelöste Übung zur Dynamik
Werbung   

Ein Körper mit einer Masse von 3 kg befindet sich zunächst in Ruhe auf einer vollkommen glatten horizontalen Oberfläche. Eine konstante horizontale Kraft von 4,5 N wirkt 20 s lang auf den Körper ein. Berechne:
a) Welche Beschleunigung erfährt der Körper während der Einwirkzeit der Kraft?
b) Welche Geschwindigkeit hat der Körper, wenn die Kraft nicht mehr wirkt?
c) Welche Strecke legt der Körper zurück, bis die Kraft nicht mehr wirkt?

 

Gegebene Daten:

  • Masse des Körpers:    m = 3 kg;
  • Anfangsgeschwindigkeit des Körpers:    v0 = 0;
  • Auf den Körper wirkende Kraft:    F = 4,5 N;
  • Zeitintervall, in dem die Kraft wirkt:    t = 20 s.

Schema des Problems:

Wir wählen ein nach rechts orientiertes Bezugssystem, wobei sich der Körper anfangs in Ruhe im Ursprung befindet (Abbildung 1).

Abb. 1

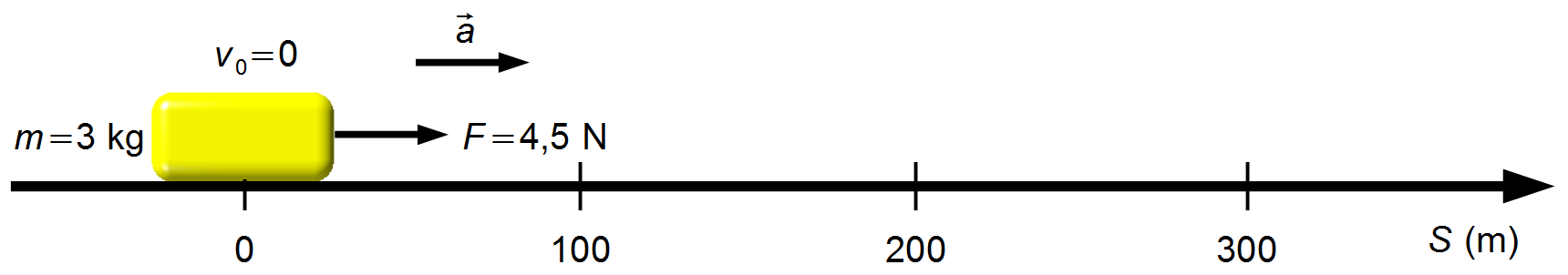
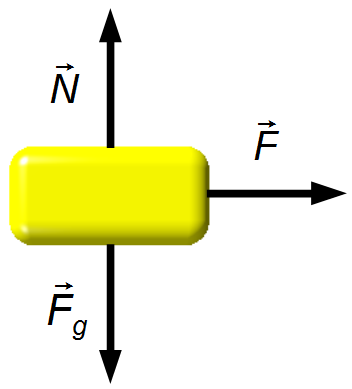
Durch das Zeichnen eines Freikörperdiagramms erhalten wir die auf die Blöcke wirkenden Kräfte (Abbildung 2).

  • Horizontale Richtung:
    • \( \vec F \) : auf den Körper wirkende Kraft.
  • Vertikale Richtung:
    • \( \vec N \) : Normalkraft der Oberfläche auf den Körper;
    • \( {\vec F}_g \) : Gewichtskraft des Körpers.
Abb. 2

Lösung:

a) Anwendung des 2. Newtonschen Gesetzes

\[ \begin{gather} \bbox[#99CCFF,10px] {\vec F=m\vec a} \end{gather} \]

In vertikaler Richtung erfolgt keine Bewegung, die Normalkraft und die Gewichtskraft heben einander auf.
In horizontaler Richtung wirkt nur die auf den Körper ausgeübte Kraft, die daher die resultierende Kraft in dieser Richtung ist

\[ \begin{gather} a=\frac{F}{m} \\[5pt] a=\frac{4,5}{3} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {a=1,5\;\text{m/s^2}} \end{gather} \]

 

b) Da der Körper eine konstante Beschleunigung erfährt, handelt es sich um eine Gleichmäßig Beschleunigte Geradlinige Bewegung. Wir wenden die Gleichung für die Geschwindigkeit als Funktion der Zeit an.

\[ \begin{gather} \bbox[#99CCFF,10px] {v=v_0+at} \end{gather} \]
\[ \begin{gather} v=0+1,5\times 20 \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {v=30\;\text{m/s}} \end{gather} \]

 

c) Wir wenden die Gleichung für die Geschwindigkeit als Funktion der Zeit auf die Gleichmäßig Beschleunigte Geradlinige Bewegung an.

\[ \begin{gather} \bbox[#99CCFF,10px] {S=S_0+v_0t+\frac{a}{2}\;t^2} \end{gather} \]
\[ \begin{gather} S=0+0\times 20+\frac{1}{2}\times 1,5\times 20^{2} \\[5pt] S=\frac{1}{\cancel 2}\times 1,5\times \cancelto{200}{400} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {S=300\;\text m} \end{gather} \]
Werbung   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .