Exercice Résolu sur la Dynamique
publicité   

Un corps de masse 3 kg, initialement au repos, repose sur une surface horizontale parfaitement lisse. Une force horizontale d'intensité constante égale à 4,5 N agit sur le corps pendant 20 s. Calculer:
a) Quelle est l'accélération acquise par le corps durant le temps où la force agit?
b) Quelle est la vitesse du corps lorsque la force cesse d'agir?
c) Quelle est la distance parcourue par le corps jusqu'à ce que la force cesse d'agir?

 

Données du problème:

  • Masse du corps:    m = 3 kg;
  • Vitesse initiale du corps:    v0 = 0;
  • Force appliquée au corps:    F = 4,5 N;
  • Intervalle de temps pendant lequel la force agit sur le corps:    t = 20 s.

Schéma du problème:

Nous choisissons un référentiel orienté vers la droite avec le corps initialement au repos à l'origine (Figure 1).

Figure 1

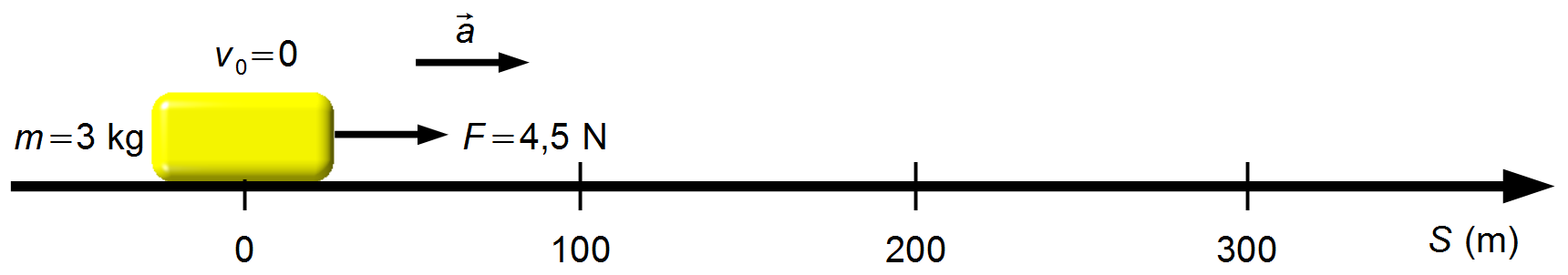
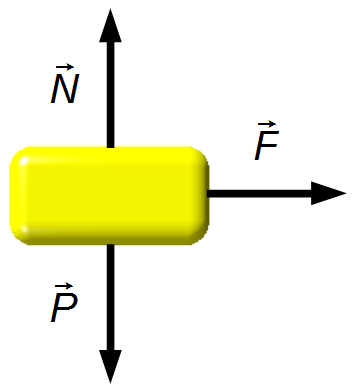
En faisant un Diagramme de Corps Libre, nous avons les forces agissant sur le bloc (Figure 2).

  • Direction horizontale:
    • \( \vec F \) : force appliquée au corps.
  • Direction verticale:
    • \( \vec N \) : force de réaction normale de la surface sur le corps;
    • \( \vec P \) : poids du corps.
Figure 2

Solution:

a) En appliquant la Deuxième Loi de Newton

\[ \begin{gather} \bbox[#99CCFF,10px] {\vec F=m\vec a} \end{gather} \]

Dans la direction verticale, il n'y a pas de mouvement, la réaction et le poids s'annulent.
Dans la direction horizontale, la seule force qui existe est la force appliquée au corps, qui sera la résultante dans cette direction, en module

\[ \begin{gather} a=\frac{F}{m} \\[5pt] a=\frac{4,5}{3} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {a=1,5\;\mathrm{m/s^2}} \end{gather} \]

 

b) Comme le corps est en accélération constante, il est en Mouvement Rectiligne Uniformément Varié, en appliquant la fonction horaire de la vitesse

\[ \begin{gather} \bbox[#99CCFF,10px] {v=v_0+at} \end{gather} \]
\[ \begin{gather} v=0+1,5\times 20 \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {v=30\;\mathrm{m/s}} \end{gather} \]

 

c) En appliquant l'équation du mouvement pour le Mouvement Rectiligne Uniformément Varié

\[ \begin{gather} \bbox[#99CCFF,10px] {S=S_0+v_0t+\frac{a}{2}\;t^2} \end{gather} \]
\[ \begin{gather} S=0+0\times 20+\frac{1}{2}\times 1,5\times 20^{2} \\[5pt] S=\frac{1}{\cancel 2}\times 1,5\times \cancelto{200}{400} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {S=300\;\mathrm m} \end{gather} \]
publicité   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .