Un corpo di massa 3 kg, inizialmente in quiete, si trova su una superficie orizzontale perfettamente liscia. Una forza orizzontale di intensità costante pari a 4,5 N agisce sul corpo per 20 s. Calcolare:
a) Qual è l’accelerazione acquisita dal corpo durante il tempo in cui la forza agisce?
b) Qual è la velocità del corpo quando la forza cessa di agire?
c) Qual è la distanza percorsa dal corpo fino a quando la forza cessa di agire?

 

Dati del problema:

• Massa del corpo:    m = 3 kg;
• Velocità iniziale del corpo:    v₀ = 0;
• Forza applicata al corpo:    F = 4,5 N;
• Intervallo di tempo in cui la forza agisce sul corpo:    t = 20 s.

Schema del problema:

Scegliamo un sistema di riferimento orientato verso destra, con il corpo inizialmente in quiete nell’origine (Figura 1).

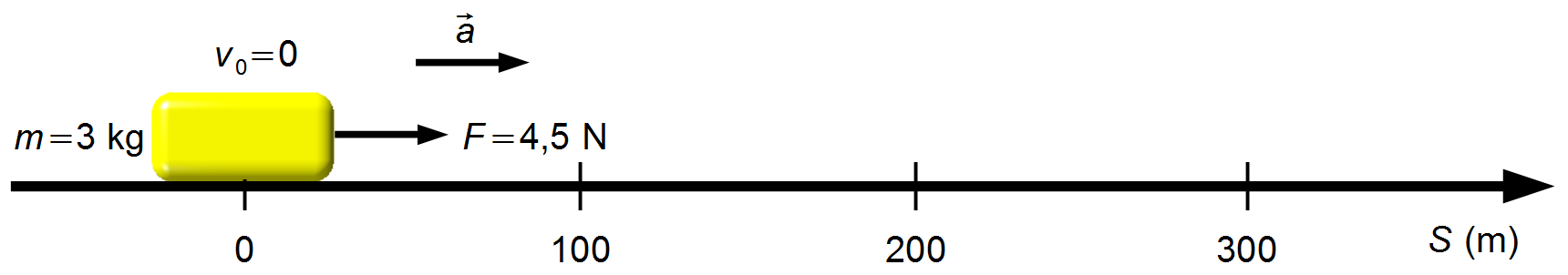
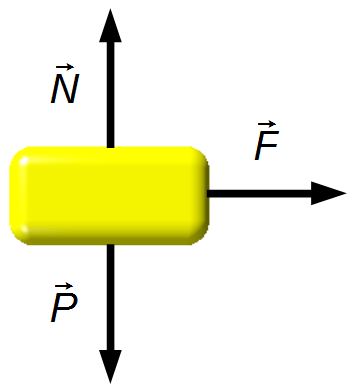
Facendo un Diagramma di Corpo Libero, abbiamo le forze che agiscono sul blocco (Figura 2).

Soluzione:

a) Applicando la Seconda Legge di Newton

Nella direzione verticale, non c’è movimento, la forza normale e la forza peso si annullano.
Nella direzione orizzontale, l’unica forza che esiste è la forza applicata al corpo, che sarà la risultante in questa direzione, in modulo

 

b) Poiché il corpo è soggetto ad accelerazione costante, esso si trova in Moto Rettilineo Uniformemente Accelerato, applicando la legge oraria della velocità

 

c) Applicando la legge oraria dello spazio percorso per il Moto Rettilineo Uniformemente Accelerato