Gelöste Übung zur Dynamik
Werbung   

In einer Atwoodschen Maschine befinden sich zwei Körper auf einer horizontalen Oberfläche, verbunden durch ein Seil, das als ideal (masselos und nicht dehnbar) angenommen wird und über eine reibungsfreie, masselose Rolle läuft. Gegeben seien die Massen ma = 24 kg und mb = 40 kg. Bestimmen Sie die Beschleunigungen der Körper, wenn:
a) F = 400 N;
b) F = 720 N;
c) F = 1200 N.

 

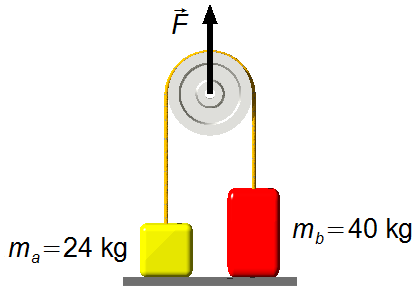
Gegebene Daten:

  • Masse des Körpers A:    ma = 24 kg;
  • Masse des Körpers B:    mb = 40 kg;
  • Erdbeschleunigung:    g = 9,8 m/s2.

Schema des Problems:

Wir wählen ein Bezugssystem, das positiv in Richtung der Kraft \( \vec F \) orientiert ist.
Die an der Rolle angreifende Kraft wird gleichmäßig auf beide Seiten verteilt (Abbildung 1-A), sodass auf jeder Seite der Rolle eine Kraft \( \frac{\vec F}{2} \) wirkt.

Abb. 1

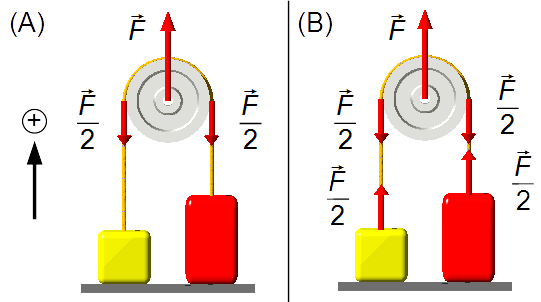
Da das Seil ideal, masselos und unelastisch ist, überträgt es lediglich die Kraft an der Umlenkrolle. Somit wird die Kraft jeder \( \vec F \) Seite der Umlenkrolle \( \frac{\vec F}{2} \) sein (Abbildung 1-B).
Durch das Zeichnen eines Freikörperdiagramms erhalten wir die auf die Blöcke wirkenden Kräfte

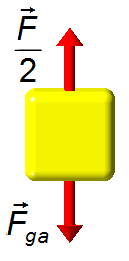
  • Körper A (Abbildung 2):
    • \( \dfrac{\vec F}{2} \): von der Rolle übertragene Kraft;
    • \( {\vec F}_{ga} \): Gewichtskraft von Körper A.
Abb. 2
  • Körper B (Abbildung 3):
    • \( \dfrac{\vec F}{2} \): von der Rolle übertragene Kraft;
    • \( {\vec F}_{gb} \): Gewichtskraft von Körper B.
Abb. 3

Lösung:

Anwendung des 2. Newtonschen Gesetzes

\[ \begin{gather} \bbox[#99CCFF,10px] {\vec F=m\vec a} \end{gather} \]
  • Körper A:
\[ \begin{gather} \frac{F}{2}-F_{ga}=m_aa_a \tag{I} \end{gather} \]
  • Körper B:
\[ \begin{gather} \frac{F}{2}-F_{gb}=m_ba_b \tag{II} \end{gather} \]

Die Gewichtskraft wird durch

\[ \begin{gather} \bbox[#99CCFF,10px] {F_g=mg} \end{gather} \]

für die Körper A und B

\[ \begin{gather} F_{ga}=m_ag \tag{III} \\[10pt] F_{gb}=m_bg \tag{IV} \end{gather} \]

Einsetzen der Gleichung (III) in die Gleichung (I)

\[ \begin{gather} \frac{F}{2}-m_ag=m_aa_a \tag{V} \end{gather} \]

Einsetzen der Gleichung (IV) in die Gleichung (II)

\[ \begin{gather} \frac{F}{2}-m_bg=m_ba_b \tag{VI} \end{gather} \]

a) Für   \( F=400\;\text N \),   ergibt sich die Beschleunigung von Körper A aus Gleichung (V)

\[ \begin{gather} a_a=\frac{\dfrac{400}{2}-24\times 9,8}{24} \\[5pt] a_a=-{\frac{35,2}{24}} \\[5pt] a_a=-1,5\;\mathrm{m/s^2} \end{gather} \]

Für Körper B mit Gleichung (VI)

\[ \begin{gather} a_b=\frac{\dfrac{400}{2}-40\times 9,8}{40}\\[5pt] a_b=-{\frac{192}{40}}\\[5pt] a_b=-4,8\;\mathrm{m/s^2} \end{gather} \]
Da die Beschleunigungen negativ sind, bewegen sich die Körper entgegen der Orientierung des Bezugssystems (nach unten), doch da sie sich auf einer Oberfläche befinden, bleiben sie in Ruhe und ihre Beschleunigungen sind null
\[ \begin{gather} \bbox[#FFCCCC,10px] {a_a=a_b=0} \end{gather} \]
Abb. 4

 

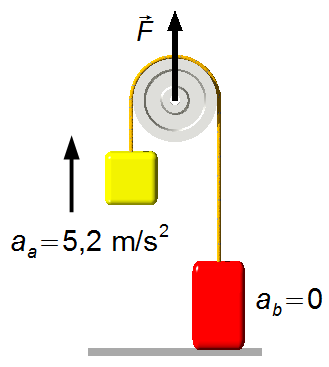
b) Für   \( F=720\;\text N \),   ergibt sich die Beschleunigung von Körper A aus Gleichung (V)

\[ \begin{gather} a_a=\frac{\dfrac{720}{2}-24\times 9,8}{24} \\[5pt] a_a=\frac{124,8}{24} \\[5pt] a_a=5,2\;\mathrm{m/s^2} \end{gather} \]

Für Körper B mit Gleichung (VI)

\[ \begin{gather} a_b=\frac{\dfrac{720}{2}-40\times 9,8}{40} \\[5pt] a_b=-{\frac{32}{40}} \\[5pt] a_b=-0,8\;\mathrm{m/s^2} \end{gather} \]
Körper A hat eine Beschleunigung von
\[ \begin{gather} \bbox[#FFCCCC,10px] {a_a=5,2\;\mathrm{m/s^2}} \end{gather} \]
Da die Beschleunigung von Körper B negativ ist, würde er sich entgegen der Orientierung des Bezugssystems bewegen (nach unten), bleibt jedoch wegen der Unterlage in Ruhe, also ist seine Beschleunigung null
\[ \begin{gather} \bbox[#FFCCCC,10px] {a_b=0} \end{gather} \]
Abb. 5

 

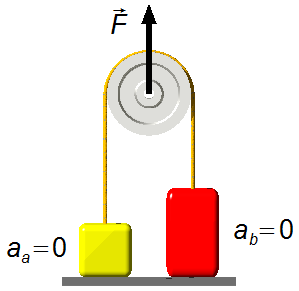
c) Für   \( F=1200\;\text N \),   ergibt sich die Beschleunigung von Körper A aus Gleichung (V)

\[ \begin{gather} a_a=\frac{\dfrac{1200}{2}-24\times 9,8}{24} \\[5pt] a_a=\frac{364,8}{24} \\[5pt] a_a=15,2\;\mathrm{m/s^2} \end{gather} \]
Für Körper B mit Gleichung (VI)
\[ \begin{gather} a_b=\frac{\dfrac{1200}{2}-40\times 9,8}{40} \\[5pt] a_b=\frac{208}{40} \\[5pt] a_b=4,3\;\mathrm{m/s^2} \end{gather} \]
Abb. 6

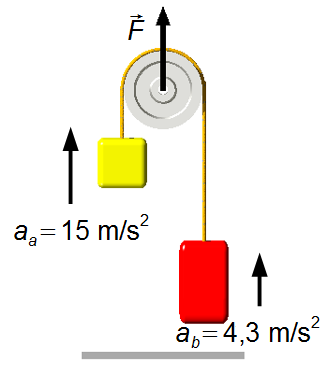
Körper A hat eine Beschleunigung von

\[ \begin{gather} \bbox[#FFCCCC,10px] {a_a=15,2\;\mathrm{m/s^2}} \end{gather} \]

und Körper B hat eine Beschleunigung von

\[ \begin{gather} \bbox[#FFCCCC,10px] {a_b=4,3\;\mathrm{m/s^2}} \end{gather} \]
Werbung   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .