Esercizio Risolto di Dinamica
pubblicità   

In una macchina di Atwood i due corpi, appoggiati su una superficie orizzontale, sono collegati da una fune, di massa trascurabile e inestensibile, che passa attraverso una carrucola, priva di inerzia e di attrito. Date le masse ma = 24 kg e mb = 40 kg. Determinare le accelerazioni dei corpi quando:
a) F = 400 N;
b) F = 720 N;
c) F = 1200 N.

 

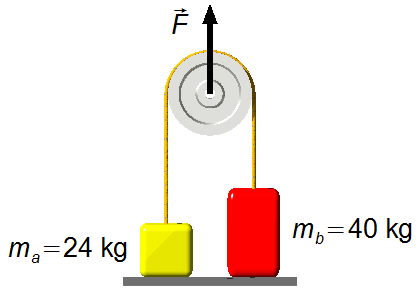
Dati del problema:

  • Massa del corpo A:    ma = 24 kg;
  • Massa dek corpo B:    mb = 40 kg;
  • Accelerazione di gravità:    g = 9,8 m/s2.

Schema del problema:

Scegliamo un sistema di riferimento orientato positivamente nello stesso senso della forza \( \vec F \).
La forza applicata a una carrucola si divide ugualmente tra i due lati (Figura 1-A), quindi la forza su ciascun lato della carrucola sarà \( \frac{\vec F}{2} \).

Figura 1

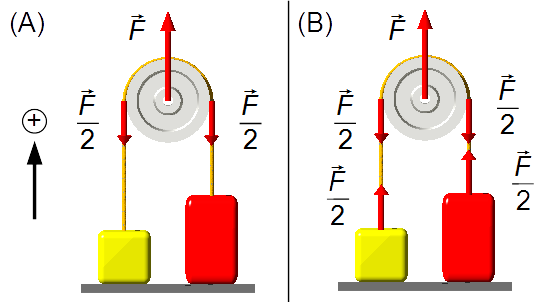
Poiché la fune è ideale, di massa trascurabile e inestensibile, essa trasmette soltanto la forza dalla carrucola ai corpi. La componente della forza \( \vec F \) su ciascun corpo sarà \( \frac{\vec F}{2} \) (Figura 1-B).
Facendo un Diagramma del Corpo Libero, abbiamo le forze che agiscono sui blocchi.

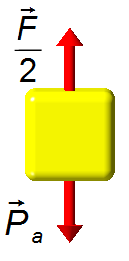
  • Corpo A (Figura 2):
    • \( \dfrac{\vec F}{2} \): forza trasmessa dalla carrucola;
    • \( {\vec P}_a \): peso del corpo A.
Figura 2
  • Corpo B (Figura 3):
    • \( \dfrac{\vec F}{2} \): forza trasmessa dalla carrucola;
    • \( {\vec P}_b \): peso del corpo B.
Figura 3

Soluzione

Applicando la Seconda Legge di Newton

\[ \begin{gather} \bbox[#99CCFF,10px] {\vec F=m\vec a} \end{gather} \]
  • Corpo A:
\[ \begin{gather} \frac{F}{2}-P_a=m_aa_a \tag{I} \end{gather} \]
  • Corpo B:
\[ \begin{gather} \frac{F}{2}-P_b=m_ba_b \tag{II} \end{gather} \]

La forza peso è data da

\[ \begin{gather} \bbox[#99CCFF,10px] {P=mg} \end{gather} \]

per i corpi A e B

\[ \begin{gather} P_a=m_ag \tag{III} \\[10pt] P_b=m_bg \tag{IV} \end{gather} \]

sostituendo l’equazione (III) nell’equazione (I)

\[ \begin{gather} \frac{F}{2}-m_ag=m_aa_a \tag{V} \end{gather} \]

sostituendo l’equazione (IV) nell’equazione (II)

\[ \begin{gather} \frac{F}{2}-m_bg=m_ba_b \tag{VI} \end{gather} \]

a) Per   \( F=400\;\text N \),   l’accelerazione del corpo A è data dall’equazione (V)

\[ \begin{gather} a_a=\frac{\dfrac{400}{2}-24\times 9,8}{24} \\[5pt] a_a=-{\frac{35,2}{24}} \\[5pt] a_a=-1,5\;\mathrm{m/s^2} \end{gather} \]

L’accelerazione del corpo B è data dall’equazione (VI)

\[ \begin{gather} a_b=\frac{\dfrac{400}{2}-40\times 9,8}{40}\\[5pt] a_b=-{\frac{192}{40}}\\[5pt] a_b=-4,8\;\mathrm{m/s^2} \end{gather} \]
Poiché le accelerazioni sono negative, i corpi dovrebbero muoversi contro l’orientazione del sistema di riferimento (verso il basso), ma poiché sono su una superficie, rimangono in quiete e le loro accelerazioni sono nulle
\[ \begin{gather} \bbox[#FFCCCC,10px] {a_a=a_b=0} \end{gather} \]
Figura 4

 

b) Per   \( F=720\;\text N \),   l’accelerazione del corpo A è data dall’equazione (V)

\[ \begin{gather} a_a=\frac{\dfrac{720}{2}-24\times 9,8}{24} \\[5pt] a_a=\frac{124,8}{24} \\[5pt] a_a=5,2\;\mathrm{m/s^2} \end{gather} \]

L’accelerazione del corpo B è data dall’equazione (VI)

\[ \begin{gather} a_b=\frac{\dfrac{720}{2}-40\times 9,8}{40} \\[5pt] a_b=-{\frac{32}{40}} \\[5pt] a_b=-0,8\;\mathrm{m/s^2} \end{gather} \]
Il corpo A ha accelerazione
\[ \begin{gather} \bbox[#FFCCCC,10px] {a_a=5,2\;\mathrm{m/s^2}} \end{gather} \]
Poiché l’accelerazione del corpo B è negativa, esso dovrebbe muoversi contro l’orientazione del sistema di riferimento (verso il basso), ma poiché è su una superficie, rimane in quiete e la sua accelerazione sarà nulla
\[ \begin{gather} \bbox[#FFCCCC,10px] {a_b=0} \end{gather} \]
Figura 5

 

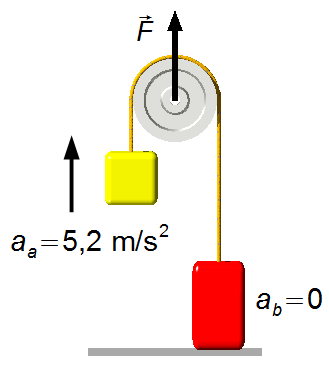
c) Per   \( F=1200\;\text N \),   l’accelerazione del corpo A è data dall’equazione (V)

\[ \begin{gather} a_a=\frac{\dfrac{1200}{2}-24\times 9,8}{24} \\[5pt] a_a=\frac{364,8}{24} \\[5pt] a_a=15,2\;\mathrm{m/s^2} \end{gather} \]
L’accelerazione del corpo B è data dall’equazione (VI)
\[ \begin{gather} a_b=\frac{\dfrac{1200}{2}-40\times 9,8}{40} \\[5pt] a_b=\frac{208}{40} \\[5pt] a_b=4,3\;\mathrm{m/s^2} \end{gather} \]
Figura 6

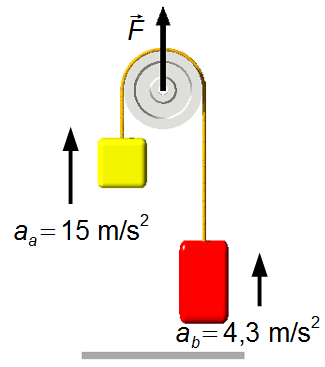
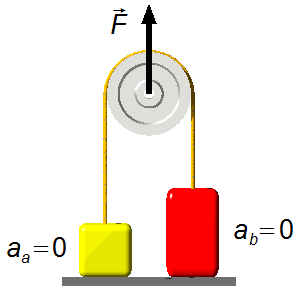
Il corpo A ha accelerazione

\[ \begin{gather} \bbox[#FFCCCC,10px] {a_a=15,2\;\mathrm{m/s^2}} \end{gather} \]

e il corpo B ha accelerazione

\[ \begin{gather} \bbox[#FFCCCC,10px] {a_b=4,3\;\mathrm{m/s^2}} \end{gather} \]
pubblicità   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .