Força Elétrica e Campo Elétrico
publicidade
Força Elétrica
Queremos repartir uma carga Q entre dois corpos. Um dos corpos recebe uma carga q1
e o outro uma carga q2. A repartição das cargas é feita de tal modo que se tenha
q1+q2=Q. Determine a razão entre as cargas para que a repulsão
coulombiana entre q1 e q2 seja máxima para qualquer distância entre as
cargas.
Duas cargas de mesmo módulo e sinais opostos estão fixas sobre uma linha horizontal a uma distância
d uma da outra. Uma esfera, de massa m carregada com uma carga elétrica, presa a um fio é
aproximada,primeiro de uma das cargas até ficar em equilíbrio exatamente sobre esta a uma altura d
da mesma. A seguir o fio é deslocado em direção a segunda carga até que a carga fique em equilíbrio sobre
a segunda carga. Encontrar os ângulos de desvio do fio nas duas situações, sabendo-se que sobre a
primeira carga o ângulo de desvio é duas vezes maior do que o ângulo de desvio sobre a segunda carga.
Campo Elétrico de Distribuições de Cargas Discretas
Duas cargas iguais de mesmo sinal estão separadas por uma distância 2d. Calcule o vetor campo
elétrico nos pontos ao longo da mediatriz da reta que une as duas cargas. Verifique a solução para pontos
muito afastados do centro do sistema.
Duas cargas iguais de mesmo sinal estão separadas por uma distância 2d. Calcule o vetor do campo
elétrico nos pontos ao longo da reta que une as duas cargas. Verifique a solução para pontos muito
afastados das cargas.
Duas cargas iguais de mesmo sinal estão separadas por uma distância 2d. O módulo do campo elétrico
nos pontos ao longo da mediatriz da reta que une as duas cargas é dado por
Determine:
a) Os pontos ao longo do eixo-y, para os quais o módulo do campo elétrico assume seu valor máximo;
b) O módulo do campo elétrico máximo.
\[
\begin{gather}
E=\frac{1}{4\pi \epsilon_0}\frac{2qy}{\left(a^2+y^2\right)^{3/2}}
\end{gather}
\]
Determine:
a) Os pontos ao longo do eixo-y, para os quais o módulo do campo elétrico assume seu valor máximo;
b) O módulo do campo elétrico máximo.
Solução
Sugestão: comparar com os pontos de máximo do campo elétrico de uma espira carregada com carga Q.
Sugestão: comparar com os pontos de máximo do campo elétrico de uma espira carregada com carga Q.
Campo Elétrico de Distribuições Contínuas de Cargas
Um aro de raio a está carregado uniformemente com uma carga Q. Calcule o vetor campo
elétrico num ponto P sobre o eixo de simetria perpendicular ao plano do aro a uma
distância z do seu centro.

Uma aro de raio a está carregado uniformemente com uma carga Q. O campo elétrico produzido por este
aro nos pontos sobre o eixo de simetria perpendicular ao plano do aro a uma distância z é dado, em
módulo, por
Determine:
a) Para quais valores de z o campo elétrico é máximo;
b) Qual é este valor máximo.
\[
\begin{gather}
E=\frac{1}{4\pi \epsilon_{0}}\frac{Qz}{\left(a^{2}+z^{2}\right)^{3/2}}
\end{gather}
\]
Determine:
a) Para quais valores de z o campo elétrico é máximo;
b) Qual é este valor máximo.
Considere dois anéis concêntricos e situados sobre o mesmo plano. O anel de raio R1
possui carga Q1, e o anel de raio R2 possui carga Q2.
O vetor campo elétrico produzido por um anel de raio r a uma distância z do centro é dado por
Determine o vetor campo elétrico:
a) No centro comum dos dois anéis;
b) Em um ponto situado a uma distância z muito maior do que R1, e do que R2.
\[
\begin{gather}
\mathbf{E}=\frac{1}{4\pi \epsilon_0}\frac{Qz}{\left(r^2+z^2\right)^{3/2}}\;\mathbf{k}
\end{gather}
\]
Determine o vetor campo elétrico:
a) No centro comum dos dois anéis;
b) Em um ponto situado a uma distância z muito maior do que R1, e do que R2.
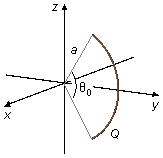
Seja um arco de circunferência de raio a e ângulo central θ0 carregado com uma
carga Q distribuída uniformemente ao longo do arco. Determine:
a) O vetor campo elétrico nos pontos da reta que passa pelo centro do arco e é perpendicular ao plano que contém o arco;
b) O vetor campo elétrico no centro de curvatura do arco;
c) O vetor campo elétrico quando o ângulo central tende a zero.
a) O vetor campo elétrico nos pontos da reta que passa pelo centro do arco e é perpendicular ao plano que contém o arco;
b) O vetor campo elétrico no centro de curvatura do arco;
c) O vetor campo elétrico quando o ângulo central tende a zero.
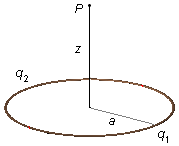
Um aro de raio a está carregado uniformemente com uma carga q1 numa das metades
do aro e outra carga q2 na outra metade. Calcule o vetor campo elétrico num ponto
P sobre o eixo de simetria perpendicular ao plano do aro a uma distância z do seu centro.
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .