Exercício Resolvido de Força Elétrica
publicidade
Duas cargas de mesmo módulo e sinais opostos estão fixas sobre uma linha horizontal a uma distância d uma da outra. Uma esfera, de massa m carregada com uma carga elétrica, presa a um fio é aproximada, primeiro de uma das cargas até ficar em equilíbrio exatamente sobre esta a uma altura d da mesma. A seguir o fio é deslocado em direção a segunda carga até que a carga fique em equilíbrio sobre a segunda carga. Encontrar os ângulos de desvio do fio nas duas situações, sabendo-se que sobre a primeira carga o ângulo de desvio é duas vezes maior do que o ângulo de desvio sobre a segunda carga.
Dados do problema:
- Distância entre as cargas na horizontal: d;
- Distância entre as cargas na vertical: d;
- Massa da esfera: m;
- Relação entre os ângulos de desvio: θ1 = 2θ2.
Adotamos que as cargas fixas, 1 e 2 na Figura 1, têm valor −Q e +Q e a carga suspensa pelo fio tem carga +q (carga 3).

Nas situações de equilíbrio temos uma distância d entre as cargas fixas na horizontal, e a carga suspensa está a uma distância d na vertical. O ângulo θ1 é o dobro de θ2, dados do problema.
Solução:
Inicialmente, a carga +q é aproximada da primeira carga −Q na vertical. Na carga +q estará atuando a força peso P, a força de tensão T1, a força elétrica de atração entre +q e −Q, F31, e a força elétrica de repulsão entre +q e +Q, F32 (Figura 2-A). As forças na vertical se equilibram, restando apenas a componente horizontal da força de repulsão F32 que desloca a carga +q da posição de equilíbrio. Para que o equilíbrio seja restabelecido, ela deve ser deslocada para a direita (Figura 2-B) até ficar na vertical sobre a carga −Q. Neste instante, o fio que prende a carga +q forma um ângulo θ1 com a vertical (Figura 2-C).
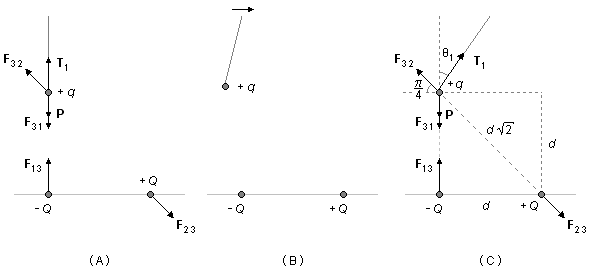
A força entre as cargas +q e −Q, F31, atua ao longo do lado do quadrado que mede d. Usando Lei de Coulomb o módulo dessa força será
\[
\begin{gather}
\bbox[#99CCFF,10px]
{F_{el}=\frac{1}{4\pi\varepsilon_0}\frac{|q_{\small A}||q_{\small B}|}{r^2}}
\end{gather}
\]
\[
\begin{gather}
F_{31}=\frac{1}{4\pi\varepsilon_0}\frac{|q_3||q_1|}{r^2}\\[5pt]
F_{31}=\frac{1}{4\pi\varepsilon_0}\frac{|q||-Q|}{d^2}\\[5pt]
F_{31}=\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2} \tag{I}
\end{gather}
\]
A força entre as cargas +q e +Q, F32, atua ao longo da diagonal de um
quadrado de lado d, formado pela distância entre as cargas +Q e −Q e pela altura
da carga +q. A diagonal vale
\( d\sqrt{2\;} \)
e esta força forma um ângulo de
\( \frac{\pi}{4} \)
com a horizontal, e o módulo será
\[
\begin{gather}
F_{32}=\frac{1}{4\pi\varepsilon_0}\frac{|q_3||q_2|}{r^2}\\[5pt]
F_{32}=\frac{1}{4\pi\varepsilon_0}\frac{|q||Q|}{\left(d\sqrt{2\;}\right)^2}\\[5pt]
F_{32}=\frac{1}{4\pi\varepsilon_0}\frac{qQ}{2d^2} \tag{II}
\end{gather}
\]
Como a esfera está em equilíbrio, a somatória das forças que atuam sobre ela é igual a zero
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\sum \mathbf F=0}
\end{gather}
\]
aplicando esta condição à situação 1 (Figura 3)
\[
\begin{gather}
\mathbf F_{32}+\mathbf T_1+\mathbf F_{31}+\mathbf P=0
\end{gather}
\]
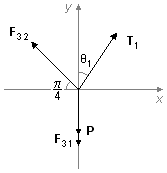
onde
\( \mathbf F_{32}=-F_{32}\cos\dfrac{\pi}{4}\;\mathbf i+F_{32}\operatorname{sen}\dfrac{\pi}{4}\;\mathbf j \)
\( \mathbf T_1=T_1\operatorname{sen}\theta_1\;\mathbf i+T_1\cos\theta_1\;\mathbf j \)
\( \mathbf F_{31}=-F_{31}\;\mathbf j \)
\( \mathbf P=-mg\;\mathbf j \)
substituindo as equações de (I) e (II)
\[
\begin{gather}
-F_{32}\cos\frac{\pi}{4}\;\mathbf i+F_{32}\operatorname{sen}\frac{\pi}{4}\;\mathbf j+T_1\operatorname{sen}\theta_1\;\mathbf i+T_1\cos\theta_1\;\mathbf j-F_{31}\;\mathbf j-mg\;\mathbf j=0\\[5pt]
-{\frac{1}{4\pi\varepsilon_0}\frac{qQ}{2d^2}\frac{\sqrt{2\;}}{2}}\;\mathbf i+\frac{1}{4\pi\varepsilon_0}\frac{qQ}{2d^2}\frac{\sqrt{2\;}}{2}\;\mathbf j+T_1\operatorname{sen}\theta_1\;\mathbf i+T_1\cos\theta_1\;\mathbf j-\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2}\;\mathbf j-mg\;\mathbf j=0
\end{gather}
\]
separando as componentes
- Direção i:
\[
\begin{gather}
-{\frac{1}{4\pi\varepsilon_0}\frac{qQ}{2d^2}\frac{\sqrt{2\;}}{2}}+T_1\operatorname{sen}\theta_1=0\\[5pt]
T_1\operatorname{sen}\theta_1=\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2}\frac{\sqrt{2\;}}{4} \tag{III}
\end{gather}
\]
- Direção j:
\[
\begin{gather}
\frac{1}{4\pi\varepsilon_0}\frac{qQ}{2d^2}\frac{\sqrt{2\;}}{2}+T_1\cos\theta_1-\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2}-mg=0\\[5pt]
T_1\cos\theta_1=\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2}-\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2}\frac{\sqrt{2\;}}{4}+mg\\[5pt]
T_1\cos\theta_1=\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2}\left(1-\frac{\sqrt{2\;}}{4}\right)+mg \tag{IV}
\end{gather}
\]
Da mesma maneira, no segundo caso, a carga +q é aproximada da segunda carga +Q na vertical.
Na carga +q estará atuando a força peso P, a força de tensão no fio, T2, a
força de atração entre +q e −Q, F31, e a força de repulsão entre
+q e +Q, F32 (Figura 4-A). As forças na vertical se equilibram, restando
apenas a componente horizontal da força de atração F31 que desloca a carga +q da
posição de equilíbrio. Para que o equilíbrio seja restabelecido ela deve ser deslocada para a direita
(Figura 4-B) até ficar na vertical sobre a carga +Q. Neste instante, o fio que prende a carga
+q forma um ângulo θ2 com a vertical (Figura 4-C).

A força entre as cargas +q e −Q, F31, atua ao longo da diagonal do quadrado, pela Lei de Coulomb o módulo dessa força será
\[
\begin{gather}
F_{31}=\frac{1}{4\pi\varepsilon_0}\frac{|q_3||q_1|}{r^2}\\[5pt]
F_{31}=\frac{1}{4\pi\varepsilon_0}\frac{|q||-Q|}{\left(d\sqrt{2\;}\right)^2}\\[5pt]
F_{31}=\frac{1}{4\pi\varepsilon_0}\frac{qQ}{2d^2} \tag{V}
\end{gather}
\]
A força entre as cargas +q e +Q, F32, será
\[
\begin{gather}
F_{32}=\frac{1}{4\pi\varepsilon_0}\frac{|q_3||q_2|}{r^2}\\[5pt]
F_{32}=\frac{1}{4\pi\varepsilon_0}\frac{|q||Q|}{d^2}\\[5pt]
F_{32}=\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2} \tag{VI}
\end{gather}
\]
Como a esfera está em equilíbrio a somatória das forças que atuam sobre ela é zero,
aplicando esta condição à situação 2 (Figura 5)
\( \mathbf F_{32}=F_{32}\;\mathbf j \)
\( \mathbf T_2=T_2\operatorname{sen}\theta_2\;\mathbf i+T_2\cos\theta_2\;\mathbf j \)
\( \mathbf F_{31}=-F_{31}\cos\dfrac{\pi}{4}\;\mathbf i-F_{31}\operatorname{sen}\dfrac{\pi}{4}\;\mathbf j \)
\( \mathbf P=-mg\;\mathbf j \)
\[
\begin{gather}
\mathbf F_{32}+\mathbf T_1+\mathbf F_{31}+\mathbf P=0
\end{gather}
\]
onde
\( \mathbf F_{32}=F_{32}\;\mathbf j \)
\( \mathbf T_2=T_2\operatorname{sen}\theta_2\;\mathbf i+T_2\cos\theta_2\;\mathbf j \)
\( \mathbf F_{31}=-F_{31}\cos\dfrac{\pi}{4}\;\mathbf i-F_{31}\operatorname{sen}\dfrac{\pi}{4}\;\mathbf j \)
\( \mathbf P=-mg\;\mathbf j \)

substituindo os valores de (V) e (VI)
\[
\begin{gather}
F_{32}\;\mathbf j+T_2\operatorname{sen}\theta_2\;\mathbf i+T_2\cos\theta_2\;\mathbf j-F_{31}\cos\frac{\pi}{4}\;\mathbf i+F_{31}\operatorname{sen}\frac{\pi}{4}\;\mathbf j-mg\;\mathbf j=0\\[5pt]
\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2}\;\mathbf j+T_2\operatorname{sen}\theta_2\;\mathbf i+T_2\cos\theta_2\;\mathbf j-\frac{1}{4\pi\varepsilon_0}\frac{qQ}{2d^2}\frac{\sqrt{2\;}}{2}\;\mathbf i-\frac{1}{4\pi\varepsilon_0}\frac{qQ}{2d^2}\frac{\sqrt{2\;}}{2}\;\mathbf j-mg\;\mathbf j=0
\end{gather}
\]
separando as componentes
- Direção i:
\[
\begin{gather}
-{\frac{1}{4\pi\varepsilon_0}\frac{qQ}{2d^2}\frac{\sqrt{2\;}}{2}}+T_2\operatorname{sen}\theta_2=0\\[5pt]
T_2\operatorname{sen}\theta_2=\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2}\frac{\sqrt{2\;}}{4} \tag{VII}
\end{gather}
\]
- Direção j:
\[
\begin{gather}
\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2}+T_2\cos\theta_2-\frac{1}{4\pi\varepsilon_0}\frac{qQ}{2d^2}\frac{\sqrt{2\;}}{2}-mg=0\\[5pt]
T_2\cos\theta_2=\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2}\frac{\sqrt{2\;}}{4}-\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2}+mg\\[5pt]
T_2\cos\theta_2=\frac{1}{4\pi\varepsilon_0}\frac{qQ}{d^2}\left(\frac{\sqrt{2\;}}{4}-1\right)+mg \tag{VIII}
\end{gather}
\]
Dividindo a equação (IV) pela equação (III)
\[
\begin{gather}
\frac{T_1\cos\theta_1}{T_1\operatorname{sen}\theta_1}=\frac{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\left(1-\dfrac{\sqrt{2\;}}{4}\right)+mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}\\[5pt]
\frac{1}{\operatorname{tg}\theta_1}=\frac{\cancel{\dfrac{1}{4\pi\varepsilon_0}}\cancel{\dfrac{qQ}{d^2}}\left(1-\dfrac{\sqrt{2\;}}{4}\right)}{\cancel{\dfrac{1}{4\pi\varepsilon_0}}\cancel{\dfrac{qQ}{d^2}}\dfrac{\sqrt{2\;}}{4}}+\frac{mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}\\[5pt]
\frac{1}{\operatorname{tg}\theta_1}=\left(1-\frac{\sqrt{2\;}}{4}\right)\frac{4}{\sqrt{2\;}}+\frac{mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}\\[5pt]
\frac{1}{\operatorname{tg}\theta_1}=\left(\frac{4}{\sqrt{2\;}}-\frac{\cancel{\sqrt{2\;}}}{\cancel{4}}\frac{\cancel{4}}{\cancel{\sqrt{2\;}}}\right)+\frac{mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}\\[5pt]
\frac{1}{\operatorname{tg}\theta_1}=\left(\frac{4}{\sqrt{2\;}}\frac{\sqrt{2\;}}{\sqrt{2\;}}-1\right)+\frac{mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}\\[5pt]
\frac{1}{\operatorname{tg}\theta_1}=\left(\frac{4\sqrt{2\;}}{2}-1\right)+\frac{mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}\\[5pt]
\frac{mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}=\left(2\sqrt{2\;}-1\right)-\frac{1}{\operatorname{tg}\theta_1} \tag{IX}
\end{gather}
\]
Dividindo a equação (VIII) pela equação (VII)
\[
\begin{gather}
\frac{T_2\cos\theta_2}{T_2\operatorname{sen}\theta_2}=\frac{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\left(\dfrac{\sqrt{2\;}}{4}-1\right)+mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}\\[5pt]
\frac{1}{\operatorname{tg}\theta_2}=\frac{\cancel{\dfrac{1}{4\pi\varepsilon_0}}\cancel{\dfrac{qQ}{d^2}}\left(\dfrac{\sqrt{2\;}}{4}-1\right)}{\cancel{\dfrac{1}{4\pi\varepsilon_0}}\cancel{\dfrac{qQ}{d^2}}\dfrac{\sqrt{2\;}}{4}}+\frac{mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}\\[5pt]
\frac{1}{\operatorname{tg}\theta_2}=\left(\frac{\sqrt{2\;}}{4}-1\right)\frac{4}{\sqrt{2\;}}+\frac{mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}\\[5pt]
\frac{1}{\operatorname{tg}\theta_2}=\left(\frac{\cancel{\sqrt{2\;}}}{\cancel{4}}\frac{\cancel{4}}{\cancel{\sqrt{2\;}}}-\frac{4}{\sqrt{2\;}}\right)+\frac{mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}\\[5pt]
\frac{1}{\operatorname{tg}\theta_2}=\left(1-\frac{4}{\sqrt{2\;}}\frac{\sqrt{2\;}}{\sqrt{2\;}}\right)+\frac{mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}\\[5pt]
\frac{1}{\operatorname{tg}\theta_2}=\left(1-\frac{4\sqrt{2\;}}{2}\right)+\frac{mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}\\[5pt]
\frac{mg}{\dfrac{1}{4\pi\varepsilon_0}\dfrac{qQ}{d^2}\dfrac{\sqrt{2\;}}{4}}=\left(1-2\sqrt{2\;}\right)-\frac{1}{\operatorname{tg}\theta_2} \tag{X}
\end{gather}
\]
Igualando as equações (IX) e (X)
\[
\begin{gather}
\left(2\sqrt{2\;}-1\right)-\frac{1}{\operatorname{tg}\theta_1}=\left(1-2\sqrt{2\;}\right)-\frac{1}{\operatorname{tg}\theta_2}\\[5pt]
\frac{1}{\operatorname{tg}\theta_1}-\frac{1}{\operatorname{tg}\theta_2}=\left(2\sqrt{2\;}-1\right)-\left(1-2\sqrt{2\;}\right)\\[5pt]
\frac{1}{\operatorname{tg}\theta_1}-\frac{1}{\operatorname{tg}\theta_2}=2\sqrt{2\;}-1-1+2\sqrt{2\;}\\[5pt]
\frac{1}{\operatorname{tg}\theta_1}-\frac{1}{\operatorname{tg}\theta_2}=4\sqrt{2\;}-2\\[5pt]
\frac{1}{\operatorname{tg}\theta_1}-\frac{1}{\operatorname{tg}\theta_2}=2\left(2\sqrt{2\;}-1\right)
\end{gather}
\]
Substituindo a condição dada no problema θ1 = 2θ2
\[
\begin{gather}
\frac{1}{\operatorname{tg}2\theta_2}-\frac{1}{\operatorname{tg}\theta_2}=2\left(2\sqrt{2\;}-1\right)
\end{gather}
\]
Da Trigonometria
\[
\begin{gather}
\operatorname{tg}(a+b)=\frac{\operatorname{tg}a+\operatorname{tg}b}{1-\operatorname{tg}a\operatorname{tg}b}
\end{gather}
\]
sendo a = b = θ2
\[
\begin{gather}
\operatorname{tg}2\theta_2=\frac{2\operatorname{tg}\theta_2}{1-\operatorname{tg}^2\theta_2}
\end{gather}
\]
\[
\begin{gather}
\frac{1}{\dfrac{2\operatorname{tg}\theta_2}{1-\operatorname{tg}^2\theta_2}}-\frac{1}{\operatorname{tg}\theta_2}=2\left(2\sqrt{2\;}-1\right)\\[5pt]
\frac{1-\operatorname{tg}^2\theta_2}{2\operatorname{tg}\theta_2}-\frac{1}{\operatorname{tg}\theta_2}=2\left(2\sqrt{2\;}-1\right)
\end{gather}
\]
multiplicando toda a equação por 2 tg θ2
\[
\begin{gather}
\qquad \qquad \qquad \frac{1-\operatorname{tg}^2\theta_2}{2\operatorname{tg}\theta_2}-\frac{1}{\operatorname{tg}\theta_2}=2\left(2\sqrt{2\;}-1\right)\qquad (\times\;2\operatorname{tg}\theta_2)\\[5pt]
\frac{1-\operatorname{tg}^2\theta_2}{\cancel{2\operatorname{tg}\theta_2}}\cancel{2\operatorname{tg}\theta_2}-\frac{1}{\cancel{\operatorname{tg}\theta_2}}2\cancel{\operatorname{tg}\theta_2}=2\left(2\sqrt{2\;}-1\right)2\operatorname{tg}\theta_2\\[5pt]
1-\operatorname{tg}^2\theta_2-2=4\left(2\sqrt{2\;}-1\right)\operatorname{tg}\theta_2\\[5pt]
-\operatorname{tg}^2\theta_2-1=4\left(2\sqrt{2\;}-1\right)\operatorname{tg}\theta_2\\[5pt]
\operatorname{tg}^2\theta_2+4\left(2\sqrt{2\;}-1\right)\operatorname{tg}\theta_2+1=0
\end{gather}
\]
fazendo a mudança de variável x = tg θ2 podemos reescrever a equação acima
\[
\begin{gather}
x^2+4\left(2\sqrt{2\;}-1\right)x+1=0
\end{gather}
\]
Solução da Equação de 2.º Grau \( x^2+4\left(2\sqrt{2\;}-1\right)x+1=0 \)
\[
\begin{array}{l}
\Delta =\left[4(2\sqrt{2\;}-1)\right]^2-4\times 1\times 1\\
\Delta =16(2\sqrt{2\;}-1)^2-4\\
\Delta=16(8-4\sqrt{2\;}+1)-4\\
\Delta =4(35-16\sqrt{2\;})\\[10pt]
x=\dfrac{-4(2\sqrt{2\;}-1)\pm\sqrt{4(35-16\sqrt{2\;})\;}}{2\times 1}
\end{array}
\]
as duas raízes da equação serão
\[
\begin{gather}
x_1=-0,1394
\\ \quad \text{e} \quad \\
x_2=-7,1743
\end{gather}
\]
para x1 teremos θ2 dado por
\[
\begin{gather}
\operatorname{tg}\theta_2=-0,1394\\[5pt]
\theta_2=\operatorname{arctg}(-0,1394)
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\theta_2=7,94°=7°56'}
\end{gather}
\]
da condição do problema temos para θ1
\[
\begin{gather}
\theta_1=2\times 7,94
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\theta_1=15,88°=15°52'}
\end{gather}
\]
para x2 teremos θ2 dado por
\[
\begin{gather}
\operatorname{tg}\theta_2=-7,1743\\[5pt]
\theta_2=\operatorname{arctg}(-7,1743)
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\theta_2=82,06°=82°03'}
\end{gather}
\]
da condição do problema temos para θ1
\[
\begin{gather}
\theta_1=2\times 82,06
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\theta_1=164,12°=164°04'}
\end{gather}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .