Exercício Resolvido de Campo Elétrico
publicidade
Duas cargas iguais de mesmo sinal estão separadas por uma distância 2d. Calcule o vetor campo elétrico nos pontos ao longo da mediatriz da reta que une as duas cargas. Verifique a solução para pontos muito afastados do centro do sistema.
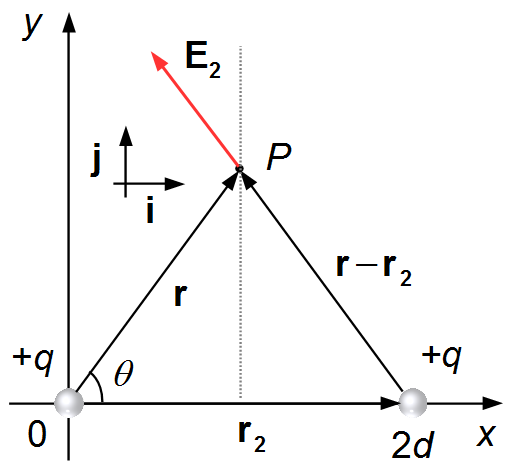
Esquema do problema:
O vetor r localiza o ponto P, onde queremos calcular o campo elétrico em relação à
origem, e é escrito como
\( \mathbf r=d\;\mathbf i+y\;\mathbf j \).
O vetor r1 vai da origem até a carga +q (Figura 1), como a carga
está localizada na origem este vetor é igual à zero,
\( \mathbf r_1=\mathbf{0} \).
O vetor r−r1 vai carga até o ponto P, neste caso
coincide com o vetor r, é dado por
\( \mathbf r-\mathbf r_1=d\;\mathbf i+y\;\mathbf j-\mathbf{0}=d\;\mathbf i+y\;\mathbf j \).

O vetor r é o mesmo da situação anterior. O vetor r2 vai da origem
até a segunda carga +q, e é dado por
\( \mathbf r_2=2d\mathbf i \).
O vetor r−r2 vai da carga até o ponto P, e é dado por
\( \mathbf r-\mathbf r_2=d\;\mathbf i+y\;\mathbf j-2d\mathbf i=-d\;\mathbf i+y\;\mathbf j \),
(Figura 2).
Solução:
O vetor campo elétrico de um sistema discreto de cargas é dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\mathbf E=\frac{1}{4\pi\epsilon_0}\;\sum_{i=1}^n\;\frac{q_i}{\left|\mathbf r-\mathbf r_i\right|^2}\;\frac{\mathbf r-\mathbf r_i}{\left|\mathbf r-\mathbf r_i\right|}}
\end{gather}
\]
\[
\begin{gather}
\mathbf E=\frac{1}{4\pi\epsilon_0}\left\{\frac{q_1}{\left|\mathbf r-\mathbf r_1\right|^2}\;\frac{\mathbf r-\mathbf r_1}{\left|\mathbf r-\mathbf r_1\right|}+\frac{q_2}{\left|\mathbf r-\mathbf r_2\right|^2}\;\frac{\mathbf r-\mathbf r_2}{\left|\mathbf r-\mathbf r_2\right|}\right\}
\end{gather}
\]
Os denominadores da equação acima são escritos como (Figuras 1 e 2):
\( \left|\mathbf r-\mathbf r_1\right|=\sqrt{d^2+y^2\;} \)
\( \left|\mathbf r-\mathbf r_1\right|^2=d^2+y^2 \)
\( \left|\mathbf r-\mathbf r_2\right|=\sqrt{(-d)^2+y^2\;}=\sqrt{d^2+y^2\;} \)
\( \left|\mathbf r-\mathbf r_2\right|^2=d^2+y^2 \)
\[
\begin{gather}
\mathbf E=\frac{1}{4\pi\epsilon_0}\left\{\frac{q}{\left(d^2+y^2\right)^{1/2}}\;\frac{\left(d\;\mathbf i+y\;\mathbf j\right)}{\left(d^2+y^2\right)}+\frac{q}{\left(d^2+y^2\right)^{1/2}}\;\frac{\left(-d\;\mathbf i+y\;\mathbf j\right)}{\left(d^2+y^2\right)}\right\}\\[5pt]
\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{q}{\left(d^2+y^2\right)^{3/2}}\left[d\;\mathbf i+y\;\mathbf j-d\;\mathbf i-y\;\mathbf j\right]\\[5pt]
\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{2yq}{\left(d^2+y^2\right)^{3/2}}\;\mathbf j
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{2qy}{\left(d^2+y^2\right)^{3/2}}\;\mathbf j}
\end{gather}
\]
Para pontos muito afastados do centro do sistema temos, y≫d, podemos desprezar o termo em
d2 no denominador e a solução será
\[
\begin{gather}
\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{2qy}{\left(\cancel{d^2}+y^2\right)^{3/2}}\;\mathbf j\\[5pt]
\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{2qy}{y^{\cancel 2\times\frac{3}{\cancel 2}}}\;\mathbf j\\[5pt]
\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{2q\cancel y}{y^{\cancelto{2}{3}}}\;\mathbf j\\[5pt]
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{\mathbf E=\frac{1}{4\pi\epsilon_0}\frac{2q}{y^2}\;\mathbf j}
\end{gather}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .