Exercício Resolvido de Campo Magnético

Em um ponto de São Paulo (cidade brasileira), o vetor campo magnético terrestre tem módulo \( B_{\small T}=8 \pi \times 10^{–6} \mathrm T \). Neste ponto, coloca-se um solenoide, de modo que seu eixo esteja paralelo ao campo terreste \( {\vec B}_{\small T} \). O comprimento do solenoide é 0,25 m e ele possui 500 espiras. Calcule a intensidade da corrente do mesmo para que seja nulo o campo magnético no seu interior. Permeabilidade Magnética do vácuo \( \mu_0=4\pi \times 10^{-7}\;\mathrm{\frac{T.m}{A}} \).

Dados do problema:

Comprimento do solenoide: ℓ = 0,25 m;
Número de espiras do solenoide: N = 500 espiras;
Campo magnético no local: \( B_{\small T}=8 \pi \times 10^{–6} \mathrm T \);
Permeabilidade Magnética do vácuo: \( \mu_0=4\pi \times 10^{-7}\;\mathrm{\frac{T.m}{A}} \).

Esquema do problema:

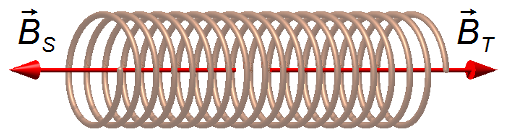
Vamos adotar a direção do campo magnético terrestre, \( {\vec B}_{\small T} \), como positivo (Figura 1).

Figura 1

Solução

O vetor resultante do campo magnético é dado por

\[ \begin{gather} \bbox[#99CCFF,10px] {\vec B={\vec B}_{\small S}+{\vec B}_{\small T}} \end{gather} \]

Em módulo, para que a resultante do campo magnético seja nulo, temos a condição

\[ \begin{gather} B_{\small T}-B_{\small S}=0 \tag{I} \end{gather} \]

O módulo do campo magnético de um solenoide é dado por

\[ \begin{gather} \bbox[#99CCFF,10px] {B_S=\mu_0\frac{N}{\ell}i} \tag{II} \end{gather} \]

substituindo a expressão (II) para o campo magnético do solenoide na equação (I)

\[ \begin{gather} B_{\small T}-\mu_{0}\frac{N}{\ell}i=0\\[5pt] i=\frac{B_{\small T} \ell}{\mu_{0} N}\\[5pt] i=\frac{8\cancel{\pi}\times10^{-6}\times 0,25}{4\cancel{\pi}\times 10^{-7}\times 500} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {i=0,01\;\mathrm A=10\;\mathrm{mA}} \end{gather} \]

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .