Solved Problem on Magnetic Field

At a point in São Paulo (a Brazilian city), the earth's magnetic field vector has magnitude \( B_{\small E}=8 \pi \times 10^{–6} \mathrm T \). At this point, a solenoid is placed so that its axis is parallel to the Earth's magnetic field \( \vec B_{\small E} \). The length of the solenoid is 0.25 m, and it has 500 turns. Calculate the magnitude of its current so that the magnetic field inside it is zero. Vacuum Magnetic Permeability   \( \mu_0=4\pi \times 10^{-7}\;\mathrm{\frac{T.m}{A}} \).

 

Problem data:

  • Solenoid length:    ℓ = 0.25 m;
  • Number of solenoid turns:    N = 500 turns;
  • Magnetic field at the location:    \( B_{\small E}=8 \pi \times 10^{–6} \mathrm T \);
  • Vacuum Magnetic Permeability:    \( \mu_0=4\pi \times 10^{-7}\;\mathrm{\frac{T.m}{A}} \).

Problem diagram:

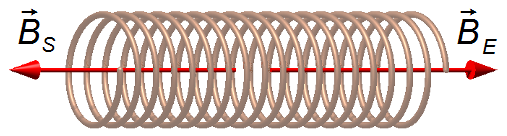
We assume the direction of the Earth's magnetic field, \( \vec B_{\small E} \), is positive (Figure 1).
Figure 1

Solution:

The resultant vector of the magnetic field is given by

\[ \begin{gather} \bbox[#99CCFF,10px] {\vec B=\vec B_{\small S}+\vec B_{\small E}} \end{gather} \]

The magnitude for the resultant of the magnetic field to be zero, we have the condition

\[ \begin{gather} B_{\small E}-B_{\small S}=0 \tag{I} \end{gather} \]

The magnitude of the magnetic field of a solenoid is given by

\[ \begin{gather} \bbox[#99CCFF,10px] {B_S=\mu_0\frac{N}{\ell}i} \tag{II} \end{gather} \]

substituting equation (II) for the solenoid magnetic field in equation (I)

\[ \begin{gather} B_{\small E}-\mu_0\frac{N}{\ell}i=0 \\[5pt] i=\frac{B_{\small E} \ell}{\mu_0 N} \\[5pt] i=\frac{\left(8\cancel{\pi}\times10^{-6}\;\mathrm{\cancel{T}}\right)\left(0.25\;\mathrm{\cancel{m}}\right)}{\left(4\pi\times 10^{-7}\;\mathrm{\frac{\cancel{T}.\cancel{m}}{A}}\right)\left(500\;\mathrm{turns}\right)} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {i=0.01\;\mathrm A=10\;\mathrm{mA}} \end{gather} \]
Note: The number of turns, 500, is a dimensionless quantity. "Turns" is not a physical quantity, which is why it does not appear in the final unit of the problem.
Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .