En un punto de São Paulo (ciudad brasileña), el vector del campo magnético terrestre tiene módulo \( B_{\small T}=8 \pi \times 10^{–6} \mathrm T \). En este punto, se coloca un solenoide de modo que su eje esté paralelo al campo terrestre \( \vec B_{\small T} \). La longitud del solenoide es de 0,25 m y tiene 500 espiras. Calcule la intensidad de la corriente necesaria para que el campo magnético en su interior sea nulo. Permeabilidad Magnética del vacío \( \mu_0=4\pi \times 10^{-7}\;\mathrm{\frac{T.m}{A}} \).

Datos del problema:

• Longitud del solenoide:    ℓ = 0,25 m;
• Longitud del solenoide:    N = 500 espiras;
• Campo magnético en el lugar:    \( B_{\small T}=8 \pi \times 10^{–6} \mathrm T \);
• Permeabilidad Magnética del vacío:    \( \mu_0=4\pi \times 10^{-7}\;\mathrm{\frac{T.m}{A}} \).

Esquema del problema:

Considerando la dirección del campo magnético terrestre, \( \vec B_{\small T} \), como positiva (Figura 1).

Figura 1

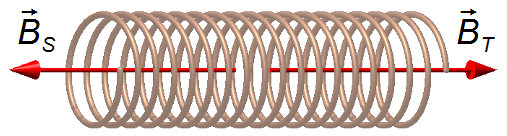
Solución:

El vector resultante del campo magnético se expresa como

En módulo, para que el resultado del campo magnético sea nulo, tenemos la condición

El módulo del campo magnético de un solenoide está dado por

sustituyendo la ecuación (II) para el campo magnético del solenoide en la ecuación (I)