Esercizio Risolto di Dinamica
pubblicità   

Due blocchi, di masse 3 kg e 2 kg, sono abbandonati a partire dal riposo in cima a un piano inclinato di 30° e percorrono una distanza di 40 m fino alla base del piano. Non esiste attrito tra i blocchi e il piano inclinato. Determinare quale dei blocchi arriverà alla fine con la maggiore velocità.

 

Dati del problema:

  • Massa del bloco A:    ma = 3 kg;
  • Massa del bloco B:    mb = 2 kg;
  • Velocità iniziale del blocco A:    v0a = 0;
  • Velocità iniziale del blocco B:    v0b = 0;
  • Lunghezza del piano inclinato:    L = 40 m;
  • Angolo di inclinazione del piano:    θ = 30°;
  • Accelerazione di gravità:    g = 9,8 m/s2.

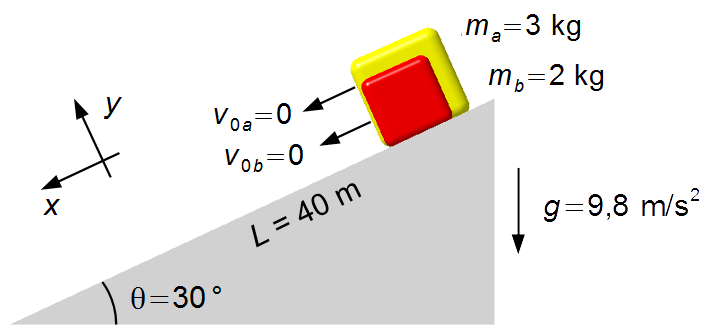
Schema del problema:

Scegliamo un sistema di riferimento orientato nel senso discendente del piano inclinato e con l’asse-x parallelo al piano (Figura 1).

Figura 1

Facendo un Diagramma del Corpo Libero, abbiamo le forze che agiscono sui blocchi.

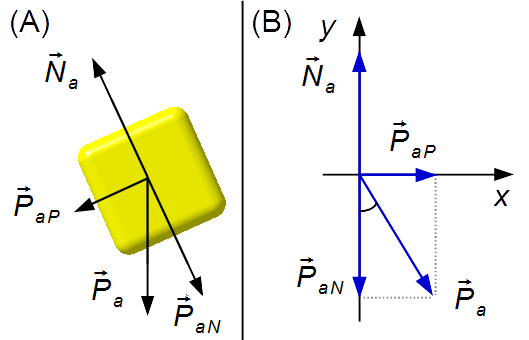
  • Blocco A (Figura 2-A):
    • \( {\vec P}_a \): peso del blocco A;
    • \( {\vec N}_a \): forza di reazione normale della superficie sul blocco A.
La forza peso può essere scomposta in due componenti, una parallela all’asse-x, \( {\vec P}_{a\small P} \), e l’altra normale o perpendicolare, \( {\vec P}_{a\small N} \) (Figura 2-A).
Disegniamo le forze in un sistema di coordinate xy (Figura 2-B)
Figura 2
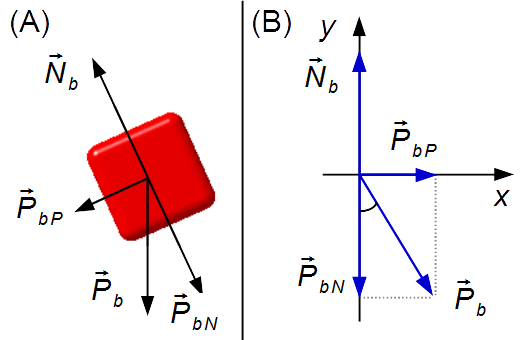
  • Blocco B (Figura 3-A):
    • \( {\vec P}_b \): peso del blocco B;
    • \( {\vec N}_b \): forza di reazione normale della superficie sul blocco B.
La forza peso può essere scomposta in due componenti, una parallela all’asse-x, \( {\vec P}_{b\small P} \), e l’altra normale o perpendicolare, \( {\vec P}_{b\small N} \) (Figura 3-A).
Disegniamo le forze in un sistema di coordinate xy (Figura 3-B)
Figura 3

Soluzione:

Applicando la Seconda Legge di Newton

\[ \begin{gather} \bbox[#99CCFF,10px] {\vec F=m\vec a} \end{gather} \]
  • Blocco A:
    • Direzione x:
\[ \begin{gather} P_{a\small P}=m_aa_a \tag{I} \end{gather} \]

la componente parallela del peso è data da

\[ \begin{gather} P_{a\small P}=P_a\operatorname{sen}\theta \tag{II} \end{gather} \]

sostituendo l’equazione (II) nell’equazione (I)

\[ \begin{gather} P_a\operatorname{sen}\theta=m_aa_a \tag{III} \end{gather} \]

la forza peso è data da

\[ \begin{gather} \bbox[#99CCFF,10px] {P=mg} \tag{IV} \end{gather} \]

per il blocco A

\[ \begin{gather} P_a=m_ag \tag{V} \end{gather} \]

Sostituendo l’equazione (V) nell’equazione (III)

\[ \begin{gather} \cancel{m_a}g\operatorname{sen}\theta =\cancel{m_a}a_a \\[5pt] a_a=g\operatorname{sen}30° \end{gather} \]
Dalla Trigonometria    \( \operatorname{sen}30°=\dfrac{1}{2} \)
\[ \begin{gather} a_a=9,8\times\frac{1}{2} \\[5pt] a_a=4,9\;\mathrm{m/s^2} \tag{VI} \end{gather} \]
  • Blocco B:
    • Direzione x:
\[ \begin{gather} P_{b\small P}=m_ba_b \tag{VII} \end{gather} \]

la componente parallela del peso è data da

\[ \begin{gather} P_{b\small P}=P_b\operatorname{sen}\theta \tag{VIII} \end{gather} \]

sostituendo l’equazione (VIII) nell’equazione (VII)

\[ \begin{gather} P_b\operatorname{sen}\theta=m_ba_b \tag{IX} \end{gather} \]

per il blocco B usando l’equazione (IV) per la forza peso

\[ \begin{gather} P_b=m_bg \tag{X} \end{gather} \]

Sostituendo l’equazione (X) nell’equazione (IX)

\[ \begin{gather} \cancel{m_b}g\operatorname{sen}\theta =\cancel{m_b}a_b \\[5pt] a_b=g\operatorname{sen}30° \\[5pt] a_b=9,8\times\frac{1}{2} \\[5pt] a_b=4,9\;\mathrm{m/s^2} \tag{XII} \end{gather} \]

Confrontando le equazioni (VI) e (XII), vediamo che i due blocchi hanno la stessa accelerazione. Poiché entrambi partono con la stessa velocità (v0a = v0b = v0 = 0) e percorrono la stessa distanza (40 m), possiamo concludere che entrambi arrivano con la stessa velocità alla fine della traiettoria.

Osservazione: Calcolando la velocità finale.
Applicando l’Equazione di Torricelli
\[ \begin{gather} \bbox[#99CCFF,10px] {v^2=v_0^2+2a\Delta S} \end{gather} \]
I due blocchi hanno la stessa accelerazione (aa = ab = a = 5 m/s2), la stessa velocità iniziale (v0a = v0b = v0 = 0) e percorrono la stessa distanza (L = 40 m). Quindi la velocità finale sarà
\[ \begin{gather} v^2=0^2+2\times 5\times 40 \\[5pt] v=\sqrt{400\;} \\[5pt] v=20\;\mathrm{m/s} \end{gather} \]
pubblicità   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .