Solved Problem on Dynamics
advertisement   

Two blocks, with masses of 3 kg and 2 kg, are released from rest at the top of a 30° inclined plane and run over a distance of 40 m to the base of the plane. The plane is frictionless. Determine which block will arrive at the end with the highest speed.

 

Problem data:

  • Mass of block A:    mA = 3 kg;
  • Mass of block B:    mB = 2 kg;
  • Initial speed of block A:    v0A = 0;
  • Initial speed of block B:    v0B = 0;
  • Length of the inclined plane:    L = 40 m;
  • Angle of the plane:    θ = 30°;
  • Acceleration due to gravity:    g = 9.8 m/s2.

Problem diagram:

We choose a reference frame oriented in the downward direction of the inclined plane and with the x-axis parallel to the plane (Figure 1).

Figure 1

Drawing a Free-Body Diagram, we have the forces acting on each block.

  • Block A (Figure 2-A):
    • \( {\vec W}_{\small A} \): weight of block A;
    • \( {\vec N}_{\small A} \): normal reaction force, surface reaction on block A.
The weight can be projected in two directions, a component parallel to the x-axis, \( {\vec W}_{\small AP} \), and the other normal or perpendicular, \( {\vec W}_{\small AN} \) (Figure 2-A).
Plotting the forces in an xy coordinate system (Figure 2-B).
Figure 2
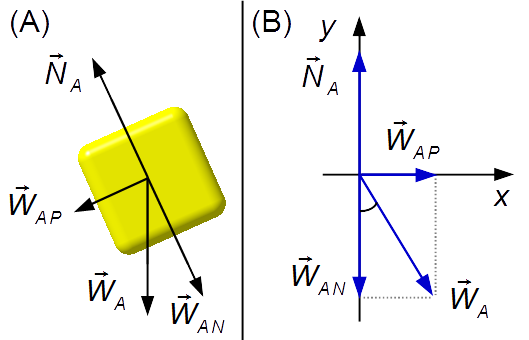
  • Block B (Figure 3-A):
    • \( {\vec W}_{\small B} \): weight of block B;
    • \( {\vec N}_{\small B} \): normal reaction force, surface reaction on block B.
The weight can be projected in two directions, a component parallel to the x-axis, \( {\vec W}_{\small BP} \), and the other normal or perpendicular, \( {\vec W}_{\small BN} \) (Figure 3-A).
Plotting the forces on an xy coordinate system (Figure 3-B).
Figure 3

Solution:

Applying Newton's Second Law

\[ \begin{gather} \bbox[#99CCFF,10px] {\vec F=m\vec a} \end{gather} \]
  • Block A:
    • x-Direction:
\[ \begin{gather} W_{\small AP}=m_{\small A}a_{\small A} \tag{I} \end{gather} \]

the parallel component of the weight is given by

\[ \begin{gather} W_{\small AP}=W_{\small A}\sin\theta \tag{II} \end{gather} \]

substituting equation (II) into equation (I)

\[ \begin{gather} W_{\small A}\sin\theta=m_{\small A}a_{\small A} \tag{III} \end{gather} \]

the weight is given by

\[ \begin{gather} \bbox[#99CCFF,10px] {W=mg} \tag{IV} \end{gather} \]

for the block A

\[ \begin{gather} W_{\small A}=m_{\small A}g \tag{V} \end{gather} \]

Substituting the equation (V) into equation (III)

\[ \begin{gather} \cancel{m_{\small A}}g\sin\theta =\cancel{m_{\small A}}a_{\small A} \\[5pt] a_{\small A}=g\sin 30° \end{gather} \]
From Trigonometry    \( \sin30°=\dfrac{1}{2} \)
\[ \begin{gather} a_{\small A}=\left(9.8\;\mathrm{m/s^2}\right)\times\frac{1}{2} \\[5pt] a_{\small A}=4.9\;\mathrm{m/s^2} \tag{VI} \end{gather} \]
  • Block B:
    • x-Direction:
\[ \begin{gather} W_{\small BP}=m_{\small B}a_{\small B} \tag{VII} \end{gather} \]

the parallel component of the weight is given by

\[ \begin{gather} W_{\small BP}=W_{\small B}\sin\theta \tag{VIII} \end{gather} \]

substituting equation (VIII) into equation (VII)

\[ \begin{gather} W_{\small B}\sin\theta=m_{\small B}a_{\small B} \tag{IX} \end{gather} \]

for block B, using equation (IV) for weight

\[ \begin{gather} W_{\small B}=m_{\small B}g \tag{X} \end{gather} \]

Substituting the equation (X) into equation (IX)

\[ \begin{gather} \cancel{m_{\small B}}g\sin\theta =\cancel{m_{\small B}}a_{\small B} \\[5pt] a_{\small B}=g\sin30° \\[5pt] a_{\small B}=\left(9.8\;\mathrm{m/s^2}\right)\times\frac{1}{2} \\[5pt] a_{\small B}=4.9\;\mathrm{m/s^2} \tag{XII} \end{gather} \]

Comparing equations (VII) and (XII), we see that the two blocks have the same acceleration. Because both start with the same initial speed and cover the same distance (40 m), we can conclude that they reach the same final speed at the end of the motion.

Note: Calculating the final speed.
Applying the equation of velocity as a function of displacement
\[ \begin{gather} \bbox[#99CCFF,10px] {v^2=v_0^2+2a\Delta S} \end{gather} \]
The two blocks have the same acceleration (aA = aB = a = 5 m/s2), the same initial speed (v0A = v0B = v0 = 0), and slid the same distance (L = 40 m) Therefore, the final speed will be
\[ \begin{gather} v^2=0^2+2\times 5\times 40 \\[5pt] v=\sqrt{400\;} \\[5pt] v=20\;\mathrm{m/s} \end{gather} \]
advertisement   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .