Gelöste Übung zur Dynamik
Werbung   

Zwei Blöcke mit den Massen 3 kg und 2 kg werden vom Ruhezustand am oberen Ende einer schiefen Ebene mit 30° Neigung losgelassen und legen bis zur Basis der Ebene eine Strecke von 40 m zurück. Zwischen den Blöcken und der schiefen Ebene gibt es keine Reibung. Bestimmen Sie, welcher der Blöcke am Ende die größere Geschwindigkeit erreicht.

 

Gegebene Daten:

  • Masse des Blocks A:    ma = 3 kg;
  • Masse des Blocks B:    mb = 2 kg;
  • Anfangsgeschwindigkeit des Blocks A:    v0a = 0;
  • Anfangsgeschwindigkeit des Blocks B:    v0b = 0;
  • Länge der schiefen Ebene:    L = 40 m;
  • Neigungswinkel der Ebene:    θ = 30°;
  • Erdbeschleunigung:    g = 9,8 m/s2.

Schema des Problems:

Wir wählen ein Bezugssystem in Richtung der Abwärtsbewegung entlang der schiefen Ebene und mit der x-Achse parallel zur Ebene (Abbildung 1).

Abb. 1

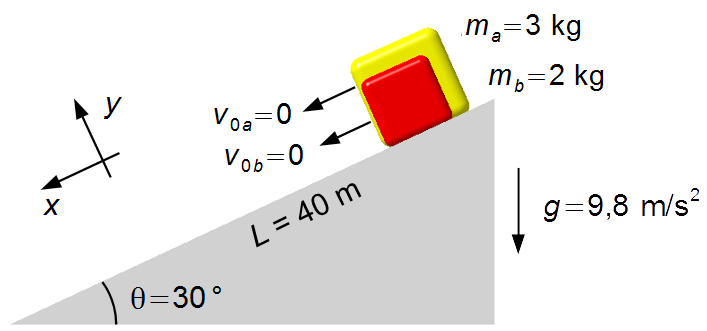
Durch das Zeichnen eines Freikörperdiagramms erhalten wir die auf die Blöcke wirkenden Kräfte.

  • Block A (Abbildung 2-A):
    • \( {\vec F}_{ga} \): Gewichtskraft des Blocks A;
    • \( {\vec N}_a \): Normalkraft der Oberfläche auf den Block A.
Die Gewichtskraft kann in zwei Komponenten zerlegt werden, eine Komponente parallel zur x-Achse, die Hangabtriebskraft \( {\vec F}_{a\small H} \), und die andere normal oder senkrecht, \( {\vec F}_{a\small N} \) (Abbildung 2-A).
Wir zeichnen die Kräfte in einem Koordinatensystem xy (Abbildung 2-B)
Abb. 2
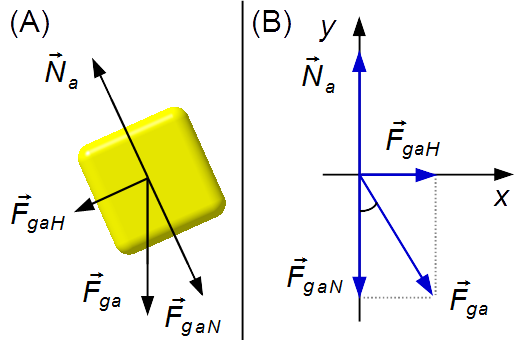
  • Block B (Abbildung 3-A):
    • \( {\vec F}_{gb} \): Gewichtskraft des Blocks B;
    • \( {\vec N}_b \): Normalkraft der Oberfläche auf den Block B.
Die Gewichtskraft kann in zwei Komponenten zerlegt werden, eine Komponente parallel zur x-Achse, die Hangabtriebskraft \( {\vec F}_{b\small H} \), und die andere normal oder senkrecht, \( {\vec P}_{b\small N} \) (Abbildung 3-A).
Wir zeichnen die Kräfte in einem Koordinatensystem xy (Abbildung 3-B)
Abb. 3

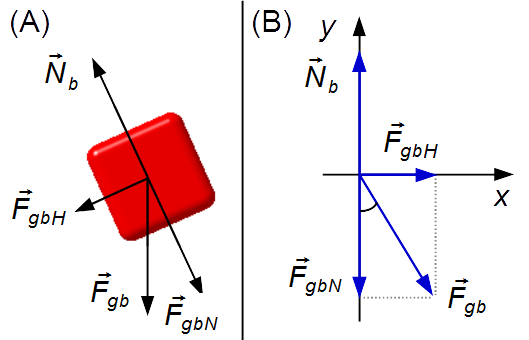
Lösung:

Anwendung des 2. Newtonschen Gesetzes

\[ \begin{gather} \bbox[#99CCFF,10px] {\vec F=m\vec a} \end{gather} \]
  • Block A:
    • x-Richtung:
\[ \begin{gather} F_{ga\small H}=m_aa_a \tag{I} \end{gather} \]

die Hangabtriebskraft ist gegeben durch

\[ \begin{gather} F_{ga\small H}=F_{ga}\sin \theta \tag{II} \end{gather} \]

Einsetzen der Gleichung (II) in die Gleichung (I)

\[ \begin{gather} F_{ga}\sin\theta=m_aa_a \tag{III} \end{gather} \]

die Gewichtskraft ist gegeben durch

\[ \begin{gather} \bbox[#99CCFF,10px] {F_g=mg} \tag{IV} \end{gather} \]

für den Block A

\[ \begin{gather} F_{ga}=m_ag \tag{V} \end{gather} \]

Einsetzen der Gleichung (V) in die Gleichung (III)

\[ \begin{gather} \cancel{m_a}g\sin\theta=\cancel{m_a}a_a \\[5pt] a_a=g\sin 30° \end{gather} \]
Aus der Trigonometrie    \( \sin 30°=\dfrac{1}{2} \)
\[ \begin{gather} a_a=9,8\times\frac{1}{2} \\[5pt] a_a=4,9\;\mathrm{m/s^2} \tag{VI} \end{gather} \]
  • Block B:
    • x-Richtung:
\[ \begin{gather} F_{gb\small H}=m_ba_b \tag{VII} \end{gather} \]

die Hangabtriebskraft ist gegeben durch

\[ \begin{gather} F_{gb\small H}=F_{gb}\sin\theta \tag{VIII} \end{gather} \]

Einsetzen der Gleichung (VIII) in die Gleichung (VII)

\[ \begin{gather} F_{gb}\sin\theta=m_ba_b \tag{IX} \end{gather} \]

für den Block B unter Verwendung der Gleichung (IV) für die Gewichtskraft

\[ \begin{gather} F_{gb}=m_bg \tag{X} \end{gather} \]

Einsetzen der Gleichung (X) in die Gleichung (IX)

\[ \begin{gather} \cancel{m_b}g\sin\theta=\cancel{m_b}a_b \\[5pt] a_b=g\sin 30° \\[5pt] a_b=9,8\times\frac{1}{2} \\[5pt] a_b=4,9\;\mathrm{m/s^2} \tag{XII} \end{gather} \]

Vergleich der Gleichungen (VI) und (XII): Wir sehen, dass beide Blöcke die gleiche Beschleunigung besitzen. Da beide mit derselben Geschwindigkeit starten (v0a = v0b = v0 = 0) und dieselbe Strecke zurücklegen (40 m), können wir schließen, dass beide am Ende der Bahn mit derselben Geschwindigkeit ankommen.

Anmerkung: Berechnung der Endgeschwindigkeit.
Anwendung der Gleichung der Geschwindigkeit als Funktion des zurückgelegten Weges
\[ \begin{gather} \bbox[#99CCFF,10px] {v^2=v_0^2+2a\Delta S} \end{gather} \]
Die beiden Blöcke haben dieselbe Beschleunigung (aa = ab = a = 5 m/s2), dieselbe Anfangsgeschwindigkeit (v0a = v0b = v0 = 0) und legen dieselbe Strecke zurück (L = 40 m). Die Endgeschwindigkeit ist daher
\[ \begin{gather} v^2=0^2+2\times 5\times 40 \\[5pt] v=\sqrt{400\;} \\[5pt] v=20\;\mathrm{m/s} \end{gather} \]
Werbung   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .