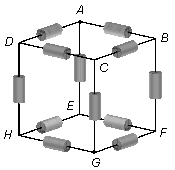
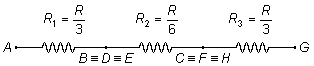On dispose de 12 résistances identiques de valeur R placées sur les arêtes d’un cube comme indiqué
sur la figure. Calculer la résistance équivalente entre les points A et G, qui forment une
des diagonales du cube.
Solution:
Le point A est un nœud du circuit, à ce point, le courant se divise également entre les
résistances placées entre les points A et B, A et D, A et E,
puisque toutes les résistances ont la même valeur R. La différence de potentiel entre chacun de
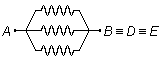
ces points est identique, par conséquent les points B, D et E représentent un même
point du circuit noté
\( B\equiv D\equiv E \),
c’est-à-dire que les trois résistances "partent" du point commun A et "arrivent" au
point commun
\( B\equiv D\equiv E \),
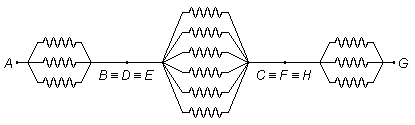
ces trois résistances sont donc en parallèle (Figure 1).
Les trois résistances placées entre les points C et G, F et G, H et
G sont également traversées par le même courant qui arrive au point G. Les points C,
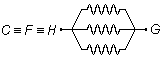
F et H représentent un même point du circuit noté
\( C\equiv F\equiv H \).
Les résistances "partent" du point commun
\( C\equiv F\equiv H \)
et "arrivent" au point commun G. Elles sont également en parallèle (Figure 2).
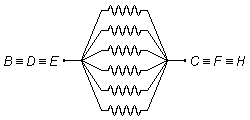
Les autres résistances sont toutes placées entre les points communs
\( B\equiv D\equiv E \)
et
\( C\equiv F\equiv H \),
elles sont toutes en parallèle (Figure 3).
Le circuit en forme de cube est équivalent à un circuit plan formé de trois résistances en parallèle, en
série avec six résistances en parallèle, puis en série avec encore trois résistances en parallèle
(Figure 4).
Appelons R1 la résistance équivalente entre les points A et
\( B\equiv D\equiv E \),
et R3 la résistance équivalente entre les points
\( C\equiv F\equiv H \)
et G. Comme ces parties du circuit sont identiques, on a
R1 = R3. La résistance équivalente d’une association de n
résistances identiques en parallèle est donnée par
\[
\begin{gather}
\bbox[#99CCFF,10px]
{R_{eq}=\frac{R}{n}}
\end{gather}
\]
pour n = 3
\[
\begin{gather}
R_1=R_3=\frac{R}{3}
\end{gather}
\]
Remarque: On pourrait également déterminer la résistance équivalente en appliquant la formule
générale pour l’association de résistances en parallèle
\[
\begin{gather}
\frac{1}{R_{eq}}=\sum_{i=1}^n{\frac{1}{R_i}} \\[5pt]
\frac{1}{R_1}=\frac{1}{R_3}=\frac{1}{R}+\frac{1}{R}+\frac{1}{R} \\[5pt]
\frac{1}{R_1}=\frac{1}{R_3}=\frac{3}{R} \\[5pt]
R_1=R_3=\frac{R}{3}
\end{gather}
\]
Entre les points
\( B\equiv D\equiv E \)
et
\( C\equiv F\equiv H \),
on a six résistances identiques en parallèle. Appelons la résistance équivalente entre ces points
R2. En appliquant à nouveau la formule pour une association en parallèle de résistances
de même valeur avec n = 6
\[
\begin{gather}
R_2=\frac{R}{6}
\end{gather}
\]
Remarque: Ou en appliquant la formule générale pour une association de résistances en parallèle
\[
\begin{gather}
\frac{1}{R_{eq}}=\sum_{i=1}^n{\frac{1}{R_i}} \\[5pt]
\frac{1}{R_2}=\frac{1}{R}+\frac{1}{R}+\frac{1}{R}+\frac{1}{R}+\frac{1}{R}+\frac{1}{R} \\[5pt]
\frac{1}{R_2}=\frac{6}{R} \\[5pt]
R_2=\frac{R}{6}
\end{gather}
\]
Ainsi, le circuit se réduit à celui-ci
La résistance équivalente du circuit Req sera la somme des résistances en série
\[
\begin{gather}
\bbox[#99CCFF,10px]
{R_{eq}=\sum_{i=1}^n{R_i}}
\end{gather}
\]
\[
\begin{gather}
R_{eq}=R_1+R_2+R_3 \\[5pt]
R_{eq}=\frac{R}{3}+\frac{R}{6}+\frac{R}{3}
\end{gather}
\]
en multipliant et en divisant le premier et le troisième terme du côté droit de l’égalité par 2
\[
\begin{gather}
R_{eq}=\frac{R}{3}\times\frac{2}{2}+\frac{R}{6}+\frac{R}{3}\times\frac{2}{2} \\[5pt]
R_{eq}=\frac{2R+R+2R}{6}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{R_{eq}=\frac{5R}{6}}
\end{gather}
\]