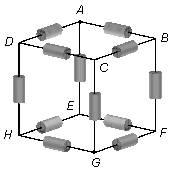
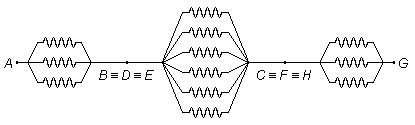
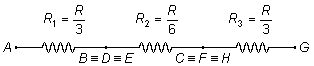Tenemos 12 resistencias iguales de valor R colocadas en las aristas de un cubo como se indica en
la figura. Calcular la resistencia equivalente entre los puntos A y G, que forman una de
las diagonales espaciales del cubo.
Solución:
El punto A es un nodo del circuito, en este punto la corriente se divide en partes iguales entre
las resistencias colocadas entre los puntos A y B, A y D, A y
E, ya que todas las resistencias tienen el mismo valor R. La caída de tensión entre cada
uno de estos puntos es la misma, por lo tanto, los puntos B, D y E representan un
mismo punto del circuito
\( B\equiv D\equiv E \),
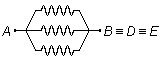
es decir, las tres resistencias "salen" del punto común A y "llegan" al punto común
\( B\equiv D\equiv E \),
por lo tanto, estas tres resistencias están en paralelo (Figura 1).
Las tres resistencias colocadas entre los puntos C y G, F y G, H y
G también son recorridas por la misma corriente que se encuentra en el punto G. Los puntos
C, F y H representan un mismo punto del circuito
\( C\equiv F\equiv H \).
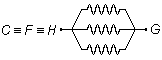
Las resistencias "salen" del punto común
\( C\equiv F\equiv H \)
y "llegan" al punto común G. Estas también están en paralelo (Figura 2).
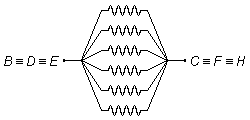
Las demás resistencias están todas colocadas entre los puntos comunes
\( B\equiv D\equiv E \)
y
\( C\equiv F\equiv H \),
y todas están en paralelo (Figura 3).
El circuito en forma de cubo es equivalente a un circuito plano formado por tres resistencias en paralelo,
en serie con seis resistencias en paralelo, y en serie con otras tres resistencias en paralelo (Figura 4).
Llamaremos R1 a la resistencia equivalente entre los puntos A y
\( B\equiv D\equiv E \),
y R3 a la resistencia equivalente entre los puntos
\( C\equiv F\equiv H \)
y G. Como estas partes del circuito son iguales, tenemos que
R1 = R3. La resistencia equivalente para una asociación de n
resistencias iguales conectadas en paralelo está dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{R_{eq}=\frac{R}{n}}
\end{gather}
\]
para n = 3
\[
\begin{gather}
R_1=R_3=\frac{R}{3}
\end{gather}
\]
Observación: También podríamos determinar la resistencia equivalente aplicando la ecuación
general para la asociación de resistencias en paralelo
\[
\begin{gather}
\frac{1}{R_{eq}}=\sum_{i=1}^n{\frac{1}{R_i}} \\[5pt]
\frac{1}{R_1}=\frac{1}{R_3}=\frac{1}{R}+\frac{1}{R}+\frac{1}{R} \\[5pt]
\frac{1}{R_1}=\frac{1}{R_3}=\frac{3}{R} \\[5pt]
R_1=R_3=\frac{R}{3}
\end{gather}
\]
Entre los puntos
\( B\equiv D\equiv E \)
e
\( C\equiv F\equiv H \)
tenemos seis resistencias iguales en paralelo; llamaremos a la resistencia equivalente entre estos
puntos R2. Aplicando nuevamente la ecuación para la asociación en paralelo de
resistencias del mismo valor con n = 6
\[
\begin{gather}
R_2=\frac{R}{6}
\end{gather}
\]
Observación: O aplicando la ecuación general para asociación de resistencias en paralelo
\[
\begin{gather}
\frac{1}{R_{eq}}=\sum_{i=1}^n{\frac{1}{R_i}} \\[5pt]
\frac{1}{R_2}=\frac{1}{R}+\frac{1}{R}+\frac{1}{R}+\frac{1}{R}+\frac{1}{R}+\frac{1}{R} \\[5pt]
\frac{1}{R_2}=\frac{6}{R} \\[5pt]
R_2=\frac{R}{6}
\end{gather}
\]
Así, el circuito se reduce al siguiente
La resistencia equivalente del circuito Req será la suma de las resistencias en serie
\[
\begin{gather}
\bbox[#99CCFF,10px]
{R_{eq}=\sum_{i=1}^n{R_i}}
\end{gather}
\]
\[
\begin{gather}
R_{eq}=R_1+R_2+R_3 \\[5pt]
R_{eq}=\frac{R}{3}+\frac{R}{6}+\frac{R}{3}
\end{gather}
\]
multiplicando y dividiendo el primer y el tercer término del lado derecho de la igualdad por 2
\[
\begin{gather}
R_{eq}=\frac{R}{3}\times\frac{2}{2}+\frac{R}{6}+\frac{R}{3}\times\frac{2}{2} \\[5pt]
R_{eq}=\frac{2R+R+2R}{6}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{R_{eq}=\frac{5R}{6}}
\end{gather}
\]