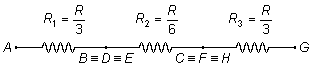Temos 12 resistores iguais de valor R colocados nas arestas de um cubo, como indicado na figura.
Calcular o resistor equivalente entre os pontos A e G que formam uma das diagonais
principais do cubo.
Solução:
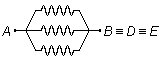
O ponto A é um nó do circuito, neste ponto a corrente se divide igualmente pelos resistores
colocados entre os pontos A e B, A e D, A e E, já que todos os
resistores têm o mesmo valor R. A queda de tensão entre cada um desses pontos é a mesma, portanto
os pontos B, D e E representam um mesmo ponto do circuito
\( B\equiv D\equiv E \),
ou seja, os três resistores "saem" do ponto em comum A e "chegam" no ponto em comum
\( B\equiv D\equiv E \),
portanto esses três resistores estão em paralelo (Figura 1).
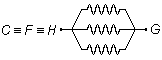
Os três resistores colocados entre os pontos C e G, F e G, H e
G também são percorridos pela mesma corrente que se encontra no ponto G, os pontos
C, F e H representam um mesmo ponto do circuito
\( C\equiv F\equiv H \).
Os resistores "saem" do ponto comum
\( C\equiv F\equiv H \)
e "chegam" no ponto comum G, estes também estão em paralelo (Figura 2).
Os demais resistores estão todos colocados entre os pontos comuns
\( B\equiv D\equiv E \)
e
\( C\equiv F\equiv H \),
estão todos em paralelo (Figura 3).
O circuito em cubo é equivalente a um circuito plano formado por três resistores em paralelo, em série com
seis resistores em paralelo e em série com mais três resistores em paralelo (Figura 4).
Vamos chamar de R1 o resistor equivalente entre os pontos A e
\( B\equiv D\equiv E \),
e de R3 o resistor equivalente entre os pontos
\( C\equiv F\equiv H \)
e G, como estas partes do circuito são iguais, temos que
R1 = R3. O resistor equivalente para uma associação e n
resistores iguais ligados em paralelo é dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{R_{eq}=\frac{R}{n}}
\end{gather}
\]
para n = 3
\[
\begin{gather}
R_1=R_3=\frac{R}{3}
\end{gather}
\]
Observação: Também poderíamos determinar o resistor equivalente aplicando a equação geral
para associação de resistores em paralelo.
\[
\begin{gather}
\frac{1}{R_{eq}}=\sum_{i=1}^n{\frac{1}{R_i}} \\[5pt]
\frac{1}{R_1}=\frac{1}{R_3}=\frac{1}{R}+\frac{1}{R}+\frac{1}{R} \\[5pt]
\frac{1}{R_1}=\frac{1}{R_3}=\frac{3}{R} \\[5pt]
R_1=R_3=\frac{R}{3}
\end{gather}
\]
Entre os pontos
\( B\equiv D\equiv E \)
e
\( C\equiv F\equiv H \)
temos seis resistores iguais em paralelo, vamos chamar o resistor equivalente entre estes pontos de
R2, aplicando novamente a equação para associação em paralelo de resistores de igual
valor com n = 6
\[
\begin{gather}
R_2=\frac{R}{6}
\end{gather}
\]
Observação: Ou aplicando a equação geral para associação de resistores em paralelo.
\[
\begin{gather}
\frac{1}{R_{eq}}=\sum_{i=1}^n{\frac{1}{R_i}} \\[5pt]
\frac{1}{R_2}=\frac{1}{R}+\frac{1}{R}+\frac{1}{R}+\frac{1}{R}+\frac{1}{R}+\frac{1}{R} \\[5pt]
\frac{1}{R_2}=\frac{6}{R} \\[5pt]
R_2=\frac{R}{6}
\end{gather}
\]
Assim, o circuito se reduz ao seguinte
O resistor equivalente do circuito Req será a soma dos resistores em série
\[
\begin{gather}
\bbox[#99CCFF,10px]
{R_{eq}=\sum_{i=1}^n{R_i}}
\end{gather}
\]
\[
\begin{gather}
R_{eq}=R_1+R_2+R_3 \\[5pt]
R_{eq}=\frac{R}{3}+\frac{R}{6}+\frac{R}{3}
\end{gather}
\]
multiplicando e dividindo o primeiro e o terceiro do lado direito da igualdade por 2
\[
\begin{gather}
R_{eq}=\frac{R}{3}\times\frac{2}{2}+\frac{R}{6}+\frac{R}{3}\times\frac{2}{2} \\[5pt]
R_{eq}=\frac{2R+R+2R}{6}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{R_{eq}=\frac{5R}{6}}
\end{gather}
\]