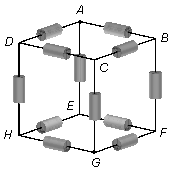
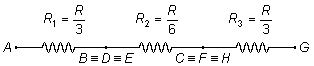We have 12 equal resistors with a value equal to R placed on the edges of a cube, as shown in the
figure. Calculate the equivalent resistance between points A and G that form one of the
main diagonals of the cube.
Solution:
Point A is a node of the circuit, at this point, the current is divided by the resistors placed
between points A and B, A and D, and between A and E since all
resistors have the same value R. The voltage drop between each of these points is the same, so
points B, D, and E represent the same point of the circuit
\( B\equiv D\equiv E \),
the three resistors "leave" the point in common A and "arrive" at the common point
\( B\equiv D\equiv E \).
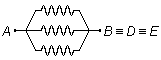
Therefore, these three resistors are in parallel (Figure 1).
The three resistors placed between the points C and G, F and G, H and
G are also traveled by the same current that is at point G. Points C, F, and
H represent the same point as the circuit
\( C\equiv F\equiv H \).
The resistors "leave" the common point
\( C\equiv F\equiv H \)
and "arrive" at the common point G. These are also in parallel (Figure 2).
The other resistors are all placed between the common points
\( B\equiv D\equiv E \)
and
\( C\equiv F\equiv H \),
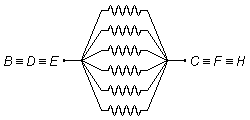
they are all in parallel (Figure 3).
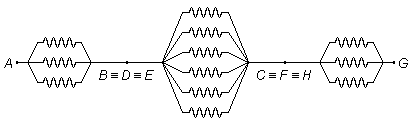
The cube circuit is equivalent to a flat circuit formed by three parallel resistors, in series with six
parallel resistors and series with three more parallel resistors (Figure 4).
Let's call R1 the equivalent resistance between points A and
\( B\equiv D\equiv E \),
and R3 the equivalent resistance between the points
\( C\equiv F\equiv H \)
and G. As these parts of the circuit are equal, we have that
R1 = R3. The equivalent resistance for an association and equal
resistors connected in parallel is given by
\[
\begin{gather}
\bbox[#99CCFF,10px]
{R_{eq}=\frac{R}{n}}
\end{gather}
\]
for n = 3
\[
\begin{gather}
R_1=R_3=\frac{R}{3}
\end{gather}
\]
Note: We could determine the equivalent resistance by applying the general expression for
resistors associated in parallel.
\[
\begin{gather}
\frac{1}{R_{eq}}=\sum_{i=1}^n{\frac{1}{R_i}} \\[5pt]
\frac{1}{R_1}=\frac{1}{R_3}=\frac{1}{R}+\frac{1}{R}+\frac{1}{R} \\[5pt]
\frac{1}{R_1}=\frac{1}{R_3}=\frac{3}{R} \\[5pt]
R_1=R_3=\frac{R}{3}
\end{gather}
\]
Between the points
\( B\equiv D\equiv E \)
and
\( C\equiv F\equiv H \),
we have six equal resistors in parallel, we will call the equivalent resistance between these
R2 points, applying the expression for association in parallel resistors of equal value
with n = 6
\[
\begin{gather}
R_2=\frac{R}{6}
\end{gather}
\]
Note: Or applying the general expression for resistors associated in parallel
\[
\begin{gather}
\frac{1}{R_{eq}}=\sum_{i=1}^n{\frac{1}{R_i}} \\[5pt]
\frac{1}{R_2}=\frac{1}{R}+\frac{1}{R}+\frac{1}{R}+\frac{1}{R}+\frac{1}{R}+\frac{1}{R} \\[5pt]
\frac{1}{R_2}=\frac{6}{R} \\[5pt]
R_2=\frac{R}{6}
\end{gather}
\]
Thus the circuit is reduced to the following
The equivalent resistance of the Req circuit will be the sum of resistors in series
\[
\begin{gather}
\bbox[#99CCFF,10px]
{R_{eq}=\sum_{i=1}^n{R_i}}
\end{gather}
\]
\[
\begin{gather}
R_{eq}=R_1+R_2+R_3 \\[5pt]
R_{eq}=\frac{R}{3}+\frac{R}{6}+\frac{R}{3}
\end{gather}
\]
multiplying and dividing the first and third terms on the right-hand side of the equation by 2
\[
\begin{gather}
R_{eq}=\frac{R}{3}\times\frac{2}{2}+\frac{R}{6}+\frac{R}{3}\times\frac{2}{2} \\[5pt]
R_{eq}=\frac{2R+R+2R}{6}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{R_{eq}=\frac{5R}{6}}
\end{gather}
\]