Exercice Résolu sur les Lois de Kirchhoff
publicité   

Dans le circuit ci-dessous, déterminer les courants dans les branches et leurs véritables sens.

 

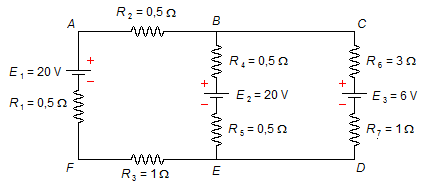
Données du problème:

Résistances:

  • R1 = 0,5 Ω;
  • R2 = 0,5 Ω;
  • R3 = 1 Ω;
  • R4 = 0,5 Ω;
  • R5 = 0,5 Ω;
  • R6 = 3 Ω;
  • R7 = 1 Ω.

Batteries:

  • E1 = 20 V;
  • E2 = 20 V;
  • E3 = 6 V;

Solution:

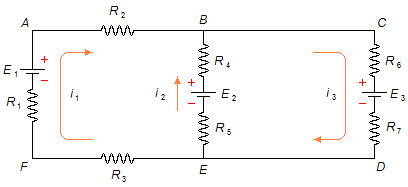
Premièrement, à chaque branche du circuit, nous attribuons, de manière aléatoire, un sens de courant. Dans la branche EFAB, nous avons le courant i1 dans le sens horaire, dans la branche BE, le courant i2 de B vers E, et dans la branche EDCB, le courant i3 dans le sens antihoraire. Ensuite, pour chaque maille du circuit, nous attribuons également un sens, de manière aléatoire, pour parcourir la maille. Pour la maille α (ABEFA), le sens est horaire, et pour la maille β (BCDEB), il est aussi horaire (Figure 1).

Figure 1
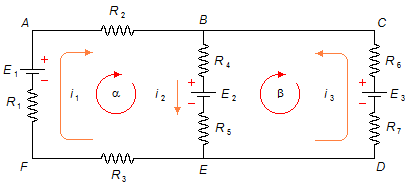
  • Application de la Loi des Nœuds
\[ \begin{gather} \bbox[#99CCFF,10px] {\sum_n i_n=0} \end{gather} \]

Les courants i1 et i3 arrivent au nœud B, et le courant i2 en sort

\[ \begin{gather} i_{2}=i_{1}+i_{3} \tag{I} \end{gather} \]
  • Application de la Loi des Mailles
\[ \begin{gather} \bbox[#99CCFF,10px] {\sum_n V_n=0} \end{gather} \]

Pour la maille α, à partir du point A dans le sens choisi, en oubliant la maille β (Figure 2)

Figure 2
\[ \begin{gather} R_2i_1+R_4i_2+E_2+R_5i_2+R_3i_1+R_1i_1-E_1=0 \end{gather} \]

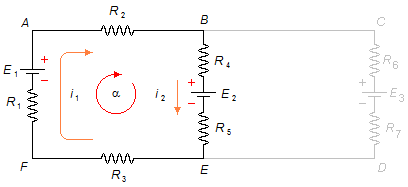
en remplaçant les valeurs du problème

\[ \begin{gather} 0,5i_1+0,5i_2+20+0,5i_2+1i_1+0,5i_1-20=0 \\[5pt] 2i_1+i_2=0 \tag{II} \end{gather} \]

Pour la maille β, à partir du point B dans le sens choisi, en oubliant la maille α (Figure 3)

Figure 3
\[ \begin{gather} -R_6i_3+E_3-R_7i_3-R_5i_2-E_2-R_4i_2=0 \end{gather} \]

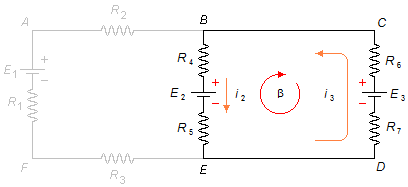
en remplaçant les valeurs

\[ \begin{gather} -3i_3+6-1i_3-0,5i_2-20-0,5i_2=0 \\[5pt] -i_2-4i_3-14=0 \\[5pt] -i_2-4i_3=14 \tag{III} \end{gather} \]

Les équations (I), (II) et (III) forment un système de trois équations à trois inconnues (i1, i2 et i3)

\[ \begin{gather} \left\{ \begin{array} \;i_2=i_1+i_3\\ \;2i_1+i_2=0\\ \;-i_2-4i_3=14 \end{array}\right. \end{gather} \]

en isolant la valeur de i1 dans la deuxième équation.

\[ \begin{gather} i_1=\frac{-{i_2}}{2} \tag{IV} \end{gather} \]

en isolant la valeur de i3 dans la troisième équation

\[ \begin{gather} i_3=\frac{-14-i_2}{4} \tag{V} \end{gather} \]

en remplaçant les expressions (IV) et (V) dans la première équation

\[ \begin{gather} i_2=\frac{-{i_2}}{2}+\frac{\left(-14-i_2\right)}{4} \\[5pt] -i_2-\frac{i_2}{2}+\frac{\left(-14-i_2\right)}{4}=0 \end{gather} \]

en multipliant l’équation par 4

\[ \begin{gather} \qquad\quad -i_2-\frac{i_2}{2}+\frac{\left(-14-i_2\;\right)}{4}=0 \qquad {\times 4} \\[5pt] -4 i_2-\cancelto{2}{4}\times\frac{i_2}{\cancel 2}+\cancel 4\times\frac{\left(-14-i_2\right)}{\cancel 4}=4\times 0 \\[5pt] -4i_2-2i_2-14-i_2=0 \\[5pt] -7i_2-14=0 \\[5pt] -7i_2=14 \\[5pt] i_2=\frac{14}{-7} \\[5pt] i_2=-2\;\mathrm A \tag{VI} \end{gather} \]

en remplaçant la valeur (VI) trouvée ci-dessus, dans les expressions (IV) et (V), nous trouvons les valeurs de i1 et i3

\[ \begin{gather} i_1=\frac{-{(-2)}}{2} \\[5pt] i_1=1\;\mathrm A \end{gather} \]
\[ \begin{gather} i_3=\frac{-14-(-2)}{4} \\[5pt] i_3=\frac{-14+2}{4} \\[5pt] i_3=\frac{-12}{4} \\[5pt] i_3=-3\;\mathrm A \end{gather} \]

Comme les valeurs des courants i2 et i3 sont négatives, cela indique que leurs véritables sens sont opposés à ceux choisis dans la Figure 1. Les valeurs des courants sont i1=1 A, i2=2 A et i3=3 A, et leurs sens sont montrés dans la Figure 4.

Figure 4
publicité   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .