Solved Problem on Kirchhoff's Laws
advertisement   



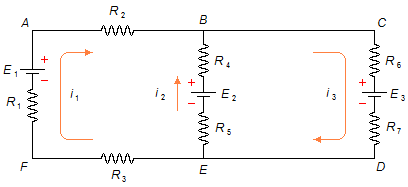
In the circuit below, find the currents and their directions.



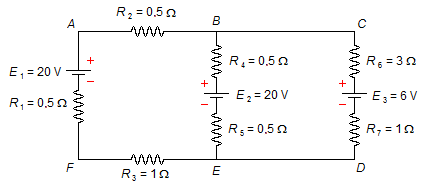
Problem data:

Resistors:
  • R1 = 0,5 Ω;
  • R2 = 0,5 Ω;
  • R3 = 1 Ω;
  • R4 = 0,5 Ω;
  • R5 = 0,5 Ω;
  • R6 = 3 Ω;
  • R7 = 1 Ω.
Batteries:
  • E1 = 20 V;
  • E2 = 20 V;
  • E3 = 6 V;
Solution

First, for each branch of the circuit, we arbitrarily choose a direction of the current. In the EFAB branch, we have the current i1 in the clockwise direction, in the branch BE the current i2 from B to E, in the branch EDCB the current i3 is in the counterclockwise direction. Second, for each loop of the circuit, we assign a direction, also arbitrarily, to traverse the mesh. The α-mesh (ABEFA) is clockwise and β-mesh (BCDEB) is also clockwise (Figure 1).
Figure 1
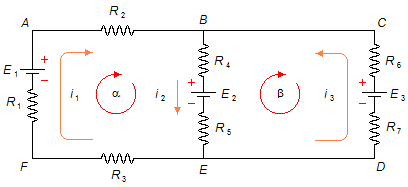
  • Using Kirchhoff's First Law
\[ \begin{gather} \bbox[#99CCFF,10px] {\sum_{n} i_{n}=0} \end{gather} \]
The currents i1 and i3 flow into node B, and the current i2 flow out of the node.
\[ \begin{gather} i_{2}=i_{1}+i_{3} \tag{I} \end{gather} \]
  • Using Kirchhoff's Second Law
\[ \begin{gather} \bbox[#99CCFF,10px] {\sum_{n} V_{n}=0} \end{gather} \]
For the α-mesh from point A in the chosen direction, forgetting the β-mesh (Figure 2)

Figure 2
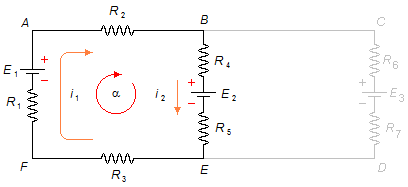
\[ \begin{gather} R_{2}i_{1}+R_{4}i_{2}+E_{2}+R_{5}i_{2}+R_{3}i_{1}+R_{1}i_{1}-E_{1}=0 \end{gather} \]
substituting the data of the problem
\[ \begin{gather} 0.5i_{1}+0.5i_{2}+20+0.5i_{2}+1i_{1}+0.5i_{1}-20=0\\[5pt] 2i_{1}+i_{2}=0 \tag{II} \end{gather} \]
For the β-mesh from point B in the chosen direction, forgetting the α-mesh (Figure 3)

Figure 3
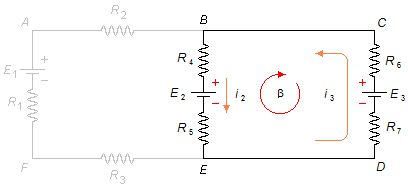
\[ \begin{gather} -R_{6}i_{3}+E_{3}-R_{7}i_{3}-R_{5}i_{2}-E_{2}-R_{4}i_{2}=0 \end{gather} \]
substituting the data
\[ \begin{gather} -3i_{3}+6-1i_{3}-0.5i_{2}-20-0.5i_{2}=0\\[5pt] -i_{2}-4i_{3}-14=0\\[5pt] -i_{2}-4i_{3}=14 \tag{III} \end{gather} \]
Equations (I), (II), and (III) can be written as a system of linear equations with three variables (i1, i2, and i3)
\[ \left\{ \begin{array} \;i_{2}=i_{1}+i_{3}\\ \;2i_{1}+i_{2}=0\\ \;-i_{2}-4i_{3}=14 \end{array} \right. \]
solving the second equation for i1
\[ \begin{gather} i_{1}=\frac{-{i_{2}}}{2} \tag{IV} \end{gather} \]
solving the third equation for i3
\[ \begin{gather} i_{3}=\frac{-14-i_{2}}{4} \tag{V} \end{gather} \]
substituting expressions (IV) and (V) into the first equation
\[ \begin{gather} i_{2}=\frac{-{i_{2}}}{2}+\frac{\left(\;-14-i_{2}\;\right)}{4}\\[5pt] -i_{2}-\frac{i_{2}}{2}+\frac{\left(\;-14-i_{2}\;\right)}{4}=0 \end{gather} \]
multiplying the equation by 4
\[ \begin{gather} \qquad\quad -i_{2}-\frac{i_{2}}{2}+\frac{\left(\;-14-i_{2}\;\right)}{4}=0 \qquad {\times 4}\\[5pt] -4 i_{2}-\cancelto{2}{4}\times \frac{i_{2}}{\cancel{2}}+\cancel{4}\times \frac{\left(\;-14-i_{2}\;\right)}{\cancel{4}}=4\times 0\\[5pt] -4i_{2}-2i_{2}-14-i_{2}=0\\[5pt] -7i_{2}-14=0\\[5pt] -7i_{2}=14\\[5pt] i_{2}=\frac{14}{-7}\\[5pt] i_{2}=-2\;\text{A} \tag{VI} \end{gather} \]
substituting the value (VI) into expressions (IV) and (V), we find the values of i1 and i3
\[ \begin{gather} i_{1}=\frac{-{(-2)}}{2}\\[5pt] i_{1}=1\;\text{A} \end{gather} \]
\[ \begin{gather} i_{3}=\frac{-14-(-2)}{4}\\[5pt] i_{3}=\frac{-14+2}{4}\\[5pt] i_{3}=\frac{-12}{4}\\[5pt] i_{3}=-3\;\text{A} \end{gather} \]
As the values of the currents, i2, and i3, are negative, this indicates that their real directions are opposite to those assumed in Figure 1. The values of the currents are i1=1 A, i2=2 A, and i3=3 A, and their directions are shown in Figure 4.

Figure 4

advertisement   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .