Ejercicio Resuelto sobre Leyes de Kirchhoff

En el circuito siguiente, determinar las corrientes en las ramas y sus verdaderos sentidos.

Datos del problema:

Resistores:

R₁ = 0,5 Ω;
R₂ = 0,5 Ω;
R₃ = 1 Ω;
R₄ = 0,5 Ω;
R₅ = 0,5 Ω;
R₆ = 3 Ω;
R₇ = 1 Ω.

Baterías:

E₁ = 20 V;
E₂ = 20 V;
E₃ = 6 V;

Solución:

En primer lugar, a cada rama del circuito le asignamos, aleatoriamente, una dirección de corriente. En la rama EFAB tenemos la corriente i₁ en sentido horario, en la rama BE la corriente i₂ de B a E y en la rama EDCB la corriente i₃ en sentido antihorario. En segundo lugar, para cada malla del circuito asignamos una dirección, también aleatoria, para recorrer la malla. Para la malla α (ABEFA) en sentido horario y para la malla β (BCDEB) también en sentido horario (Figura 1). (BCDEB) também sentido horário (Figura 1.).

Figura 1

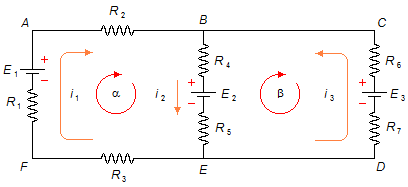
Aplicando la Ley de los Nodos

\[ \begin{gather} \bbox[#99CCFF,10px] {\sum_n i_n=0} \end{gather} \]

Las corrientes i₁ e i₃ llegan al nodo B y la corriente i₂ sale de él

\[ \begin{gather} i_{2}=i_{1}+i_{3} \tag{I} \end{gather} \]

Aplicando la Ley de las Mallas

\[ \begin{gather} \bbox[#99CCFF,10px] {\sum_n V_n=0} \end{gather} \]

Para la malla α, comenzando desde el punto A en el sentido elegido, sin tener en cuenta la malla β (Figura 2)

Figura 2

\[ \begin{gather} R_2i_1+R_4i_2+E_2+R_5i_2+R_3i_1+R_1i_1-E_1=0 \end{gather} \]

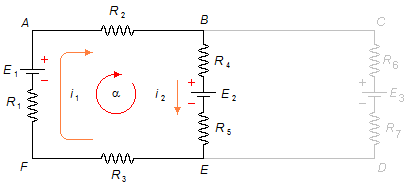
sustituyendo los valores del problema

\[ \begin{gather} 0,5i_1+0,5i_2+20+0,5i_2+1i_1+0,5i_1-20=0 \\[5pt] 2i_1+i_2=0 \tag{II} \end{gather} \]

Para la malla β, comenzando desde el punto B en el sentido elegido, sin tener en cuenta la malla α (Figura 3).

Figura 3

\[ \begin{gather} -R_6i_3+E_3-R_7i_3-R_5i_2-E_2-R_4i_2=0 \end{gather} \]

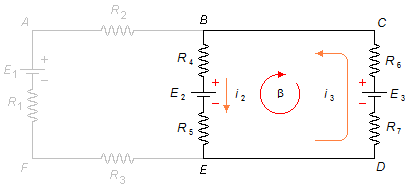
sustituyendo los valores

\[ \begin{gather} -3i_3+6-1i_3-0,5i_2-20-0,5i_2=0 \\[5pt] -i_2-4i_3-14=0 \\[5pt] -i_2-4i_3=14 \tag{III} \end{gather} \]

Las ecuaciones (I), (II) y (III) forman un sistema de tres ecuaciones con tres incógnitas (i₁, i₂ e i₃)

\[ \begin{gather} \left\{ \begin{array} \;i_2=i_1+i_3 \\ \;2i_1+i_2=0 \\ \;-i_2-4i_3=14 \end{array}\right. \end{gather} \]

aislando el valor de i₁ en la segunda ecuación

\[ \begin{gather} i_1=\frac{-{i_2}}{2} \tag{IV} \end{gather} \]

aislando el valor de i₃ en la tercera ecuación

\[ \begin{gather} i_3=\frac{-14-i_2}{4} \tag{V} \end{gather} \]

sustituyendo las expresiones (IV) y (V) en la primera ecuación

\[ \begin{gather} i_2=\frac{-{i_2}}{2}+\frac{\left(-14-i_2\right)}{4} \\[5pt] -i_2-\frac{i_2}{2}+\frac{\left(-14-i_2\right)}{4}=0 \end{gather} \]

multiplicando la ecuación por 4

\[ \begin{gather} \qquad\quad -i_2-\frac{i_2}{2}+\frac{\left(-14-i_2\;\right)}{4}=0 \qquad {\times 4} \\[5pt] -4 i_2-\cancelto{2}{4}\times\frac{i_2}{\cancel 2}+\cancel 4\times\frac{\left(-14-i_2\right)}{\cancel 4}=4.0 \\[5pt] -4i_2-2i_2-14-i_2=0 \\[5pt] -7i_2-14=0 \\[5pt] -7i_2=14 \\[5pt] i_2=\frac{14}{-7} \\[5pt] i_2=-2\;\mathrm A \tag{VI} \end{gather} \]

sustituyendo el valor (VI) encontrado anteriormente, en las expresiones (IV) y (V) encontramos los valores de i₁ e i₃

\[ \begin{gather} i_1=\frac{-{(-2)}}{2} \\[5pt] i_1=1\;\mathrm A \end{gather} \]

\[ \begin{gather} i_3=\frac{-14-(-2)}{4} \\[5pt] i_3=\frac{-14+2}{4} \\[5pt] i_3=\frac{-12}{4} \\[5pt] i_3=-3\;\mathrm A \end{gather} \]

Como el valor de las corrientes i₂ e i₃ son negativas, esto indica que sus verdaderos sentidos son contrarios a aquellos elegidos en la Figura 1. Los valores de las corrientes son i₁=1 A, i₂=2 A, e i₃=3 A, y sus sentidos están mostrados en la Figura 4.

Figura 4

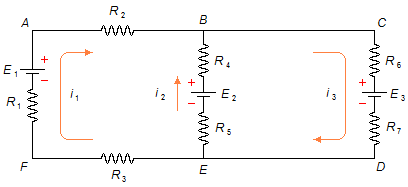
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .