Exercice Résolu sur la Dilatation Thermique

Le coefficient moyen de dilatation linéaire du fer est égal à 0,0000117 °C⁻¹. De combien doit-on augmenter la température d’un bloc de fer pour que son volume augmente de 1%?

Données du problème:

Coefficient de dilatation linéaire du fer: α = 0,0000117 °C⁻¹;
Variation de volume: ΔV = 1%.

Schéma du problème:

Figure 1

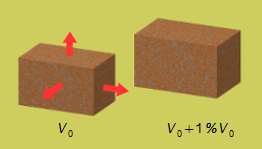
Solution:

La variation du volume sera de 1%

\[ \begin{gather} \Delta V=1V_0 \\[5pt] \Delta V=\frac{1}{100}V_0 \\[5pt] \Delta V=0,01V_0 \end{gather} \]

Le problème nous donne le coefficient de dilatation linéaire du matériau, et pour calculer l’augmentation de volume, nous avons besoin du coefficient de dilatation volumique, qui sera

\[ \begin{gather} \bbox[#99CCFF,10px] {\gamma=3\alpha} \end{gather} \]

\[ \begin{gather} \gamma=3\times 0,0000117 \\[5pt] \gamma=0,0000351 \\[5pt] \gamma=3,51\times 10^{-5}\;\mathrm{°C^{-1}} \end{gather} \]

Le volume final est donné par

\[ \begin{gather} \bbox[#99CCFF,10px] {\Delta V=\gamma V_0\Delta t} \end{gather} \]

en remplaçant les données du problème, on trouve la variation de température

\[ \begin{gather} 0,01\cancel{V_0}=3,51\times 10^{-5}\cancel{V_0}\Delta t \\[5pt] 0,01=3,51\times 10^{-5}\Delta t \\[5pt] \Delta t=\frac{0,01}{3,51\times 10^{-5}} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {\Delta t\approx 285\;\mathrm{°C}} \end{gather} \]

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .