Exercício Resolvido de Dilatação Térmica

O coeficiente de dilatação linear médio do ferro é igual a 0,0000117 °C⁻¹. De quanto deve aumentar a temperatura de um bloco de ferro para que seu volume aumente de 1%?

Dados do problema:

Coeficiente de dilatação linear do ferro: α = 0,0000117 °C⁻¹;
Variação do volume: ΔV = 1%.

Esquema do problema:

Figura 1

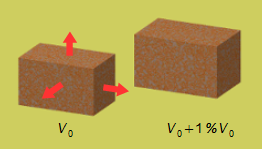
Solução:

A variação do volume será de 1%

\[ \begin{gather} \Delta V=1V_0 \\[5pt] \Delta V=\frac{1}{100}V_0 \\[5pt] \Delta V=0,01V_0 \end{gather} \]

O problema nos dá o coeficiente de dilatação linear do material e, para o cálculo do aumento de volume precisamos do coeficiente de dilatação volumétrico que será

\[ \begin{gather} \bbox[#99CCFF,10px] {\gamma=3\alpha} \end{gather} \]

\[ \begin{gather} \gamma=3\times 0,0000117 \\[5pt] \gamma=0,0000351 \\[5pt] \gamma=3,51\times 10^{-5}\;\mathrm{°C^{-1}} \end{gather} \]

O volume final é dado por

\[ \begin{gather} \bbox[#99CCFF,10px] {\Delta V=\gamma V_0\Delta t} \end{gather} \]

substituindo os dados do problema, encontramos a variação da temperatura

\[ \begin{gather} 0,01\cancel{V_0}=3,51\times 10^{-5}\cancel{V_0}\Delta t \\[5pt] 0,01=3,51\times 10^{-5}\Delta t \\[5pt] \Delta t=\frac{0,01}{3,51\times 10^{-5}} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {\Delta t\approx 285\;\mathrm{°C}} \end{gather} \]

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .