Exercice Résolu sur la Dynamique
publicité   

Dans le système de la figure, le corps A glissé sur un plan horizontal sans frottement, entraîné par corps B qui descend verticalement. Les corps A et B sont reliés l'un à l'autre par un fil inextensible de masse négligeable, parallèle au plan et passant par une poulie de masse négligeable et sans frottement. Les masses de A et B sont respectivement de 32 kg et 8 kg. Déterminer l'accélération de l'ensemble et l'intensité de la force de tension dans le fil.

 

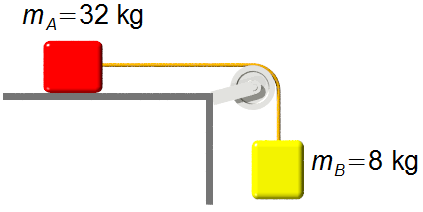
Données du problème:

  • Masse du corps A:    mA = 32 kg;
  • Masse du corps B:    mB = 8 kg;
  • Accélération de la pesanteur:    g = 9,8 m/s2.

Schéma du problème:

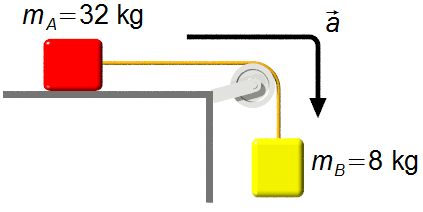
Nous choisissons un référentiel orienté vers la droite dans le même sens que l'accélération.
Figure 1

En faisant un Diagramme de Corps Libre, nous avons les forces agissant sur les blocs.

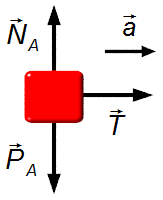
  • Corps A (Figure 2):
    • Direction verticale:
      • \( \vec P_{\small A} \): poids du corps A;
      • \( \vec N_{\small A} \): force de réaction normale de la surface sur le corps.
    • Direction horizontale:
      • \( \vec T \): force de tension dans le fil.
Figure 2
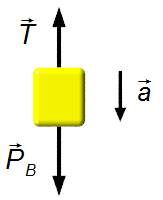
  • Corps B (Figure 3):
    • \( \vec P_{\small B} \): poids du corps B;
    • \( \vec T \): force de tension dans le fil.
Figure 3

Solution:

En appliquant la Deuxième Loi de Newton

\[ \begin{gather} \bbox[#99CCFF,10px] {\vec F=m\vec a} \end{gather} \]
  • Corps A:

Dans la direction verticale, le poids et la normale s'annulent.
Dans la direction horizontale

\[ \begin{gather} T=m_{\small A}a \tag{I} \end{gather} \]
  • Corps B:

Dans la direction horizontale, aucune force n'agit
Dans la direction verticale

\[ \begin{gather} P_{\small B}-T=m_{\small B}a \tag{II} \end{gather} \]

Le poids est donné par

\[ \begin{gather} \bbox[#99CCFF,10px] {P=mg} \end{gather} \]

pour le corps B

\[ \begin{gather} P_{\small B}=m_{\small B}g \tag{III} \end{gather} \]

en remplaçant l'équation (III) dans l'équation (II)

\[ \begin{gather} m_{\small B}g-T=m_{\small B}a \tag{IV} \end{gather} \]

Les équations (I) et (IV) forment un système de deux équations à deux inconnues (T et a). En additionnant les deux équations

\[ \begin{gather} \frac{ \left\{ \begin{array}{rr} \cancel{T}&=m_{\small A}a \\ m_{\small B}g-\cancel{T}&=m_{\small B}a \end{array} \right.} {m_{\small B}g=\left(m_{\small A}+m_{\small B}\right)a} \\[5pt] a=\frac{m_{\small B}g}{m_{\small A}+m_{\small B}} \\[5pt] a=\frac{8\times 9,8}{32+8} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {a\approx 1,9\;\mathrm{m/s^2}} \end{gather} \]

En remplaçant la masse du corps A et l'accélération trouvée ci-dessus dans la première équation du système, la tension dans le fil sera

\[ \begin{gather} T=32\times 1,9 \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {T\approx 62,7\;\mathrm N} \end{gather} \]
publicité   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .