Gelöste Übung zur Dynamik

Im System der Abbildung sind die Körper A und B mit den Massen 20 kg und 10 kg bzw. durch ein Seil verbunden. Am Seil ist ein Federkraftmesser befestigt, der anzeigt, dass die Zugkraft im Seil 100 N beträgt, und zwischen Körper A und der Ebene gibt es Reibung. Das Seil ist unelastisch und läuft über eine reibungsfreie Rolle mit vernachlässigbarer Masse. Bestimmen Sie die Beschleunigung des Systems und den Reibungskoeffizienten zwischen dem Block und der Ebene.

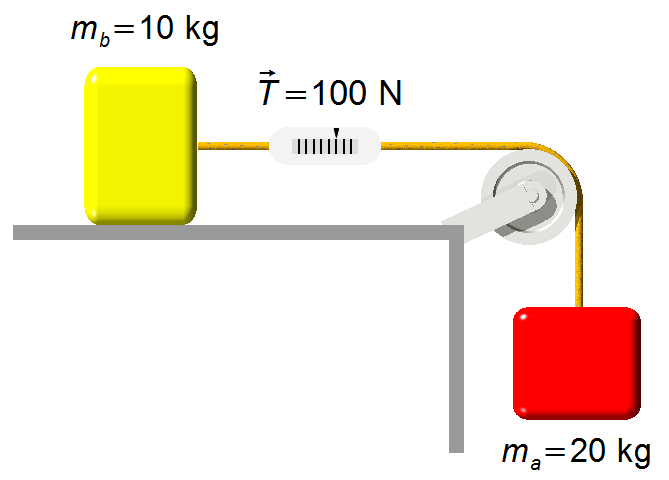
Gegebene Daten:

Masse des Körpers A: m_a = 20 kg;
Masse des Körpers B: m_b = 10 kg;
Anzeige der Zugkraft am Federkraftmesser: T = 100 N;
Erdbeschleunigung: g = 9,8 m/s².

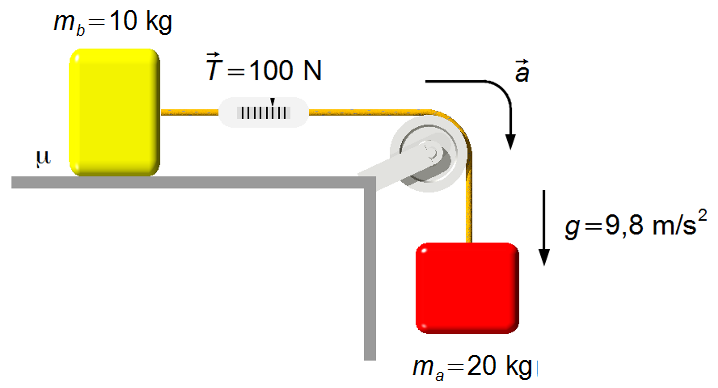
Schema des Problems:

Wir wählen ein Bezugssystem nach rechts orientiert, in derselben Richtung der Beschleunigung a, in der Körper A nach unten geht, gleiche Richtung der Erdbeschleunigung (Abbildung 1).

Abb. 1

Durch das Zeichnen eines Freikörperdiagramms erhalten wir die auf die Blöcke wirkenden Kräfte.

Block A (Abbildung 2):
- \( {\vec F}_{ga} \): Gewichtskraft des Blocks A;
- \( \vec T \): Zugkraft im Seil.

Abb. 2

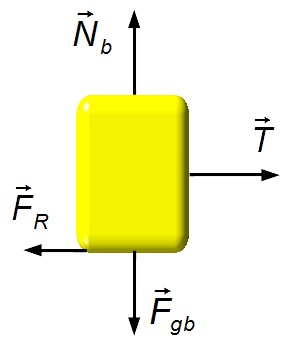
Block B (Abbildung 3):
- Vertikale Richtung:
  - \( {\vec F}_{gb} \): Gewichtskraft des Körpers B;
  - \( {\vec N}_b \): Normalkraft der Oberfläche auf den Block B.
- Horizontale Richtung:
  - \( \vec T \): Zugkraft im Seil;
  - \( {\vec F}_{\small R} \): Reibungskraft zwischen Block und Oberfläche.

Abb. 3

Lösung:

Anwenden des 2. Newtonschen Gesetzes

\[ \begin{gather} \bbox[#99CCFF,10px] {\vec F=m\vec a} \end{gather} \]

Block A:

\[ \begin{gather} F_{ga}-T=m_aa \tag{I} \end{gather} \]

Die Gewichtskraft ist gegeben durch

\[ \begin{gather} \bbox[#99CCFF,10px] {F_g=mg} \tag{II} \end{gather} \]

für den Körper A

\[ \begin{gather} F_{ga}=m_ag \tag{III} \end{gather} \]

Einsetzen der Gleichung (III) in die Gleichung (I)

\[ \begin{gather} m_ag-T=m_aa \\[5pt] a=\frac{m_ag-T}{m_a} \\[5pt] a=\frac{20\times 9,8-100}{20} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {a=4,8\;\mathrm{m/s^2}} \end{gather} \]

Block B:
- Horizontale Richtung:

Anwenden des 2. Newtonschen Gesetzes

\[ \begin{gather} T-F_{\small R}=m_ba \tag{IV} \end{gather} \]

Die Reibungskraft ist gegeben durch

\[ \begin{gather} \bbox[#99CCFF,10px] {{\vec F}_{\small R}=\mu \vec N} \end{gather} \]

für den Block B

\[ \begin{gather} F_{\small R}=\mu N_b \tag{V} \end{gather} \]

Einsetzen der Gleichung (V) in die Gleichung (IV)

\[ \begin{gather} T-\mu N_b=m_ba \tag{VI} \end{gather} \]

Block B:
- Vertikale Richtung:

In dieser Richtung gibt es keine Bewegung, die Normalkraft und die Gewichtskraft heben einander auf

\[ \begin{gather} N_b=P_b \tag{VII} \end{gather} \]

Einsetzen der Gleichung (II) für die Gewichtskraft des Körpers B

\[ \begin{gather} F_{gb}=m_bg \tag{VIII} \end{gather} \]

Einsetzen der Gleichung (VIII) in die Gleichung (VII)

\[ \begin{gather} N_b=m_bg \tag{IX} \end{gather} \]

Einsetzen der Gleichung (IX) in die Gleichung (VI), die gegebenen Daten und die oben gefundene Beschleunigung

\[ \begin{gather} T-\mu m_bg=m_ba \\[5pt] \mu=\frac{T-m_ba}{m_bg} \\[5pt] \mu=\frac{100-10\times 4,8}{10\times 9,8} \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {\mu\approx 0,5} \end{gather} \]

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .