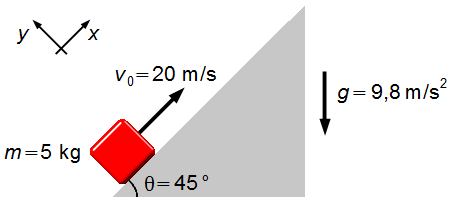
Ein Block mit der Masse 5 kg wird mit einer Anfangsgeschwindigkeit von 20 m/s in aufsteigender Richtung auf eine schiefe Ebene von 45° geworfen. Zwischen dem Block und der schiefen Ebene gibt es keine Reibung. Bestimmen Sie die Strecke, die der Block zurücklegt, bis er zum Stillstand kommt.

Gegebene Daten:

• Masse des Blocks:    m = 5 kg;
• Anfangsgeschwindigkeit des Blocks:    v₀ = 20 m/s;
• Neigungswinkel der Ebene:    θ = 45°;
• Erdbeschleunigung:    g = 9,8 m/s²;

Schema des Problems:

Wir wählen ein in aufsteigender Richtung orientiertes Bezugssystem, dessen x-Achse parallel zur Ebene liegt (Abbildung 1).

Abb. 1

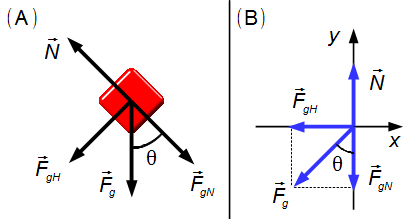
Durch Zeichnen eines Freikörperdiagramms haben wir die Kräfte, die auf den Block wirken (Abbildung 2-A).

• \( {\vec F}_g \): Gewichtskraft des Körpers;
• \( \vec N \): Normalkraft der Oberfläche auf den Körper.

Die Gewichtskraft kann in zwei Komponenten zerlegt werden, eine Komponente parallel zur x-Achse, die Hangabtriebskraft \( {\vec F}_{g\small H} \), und die andere normal oder senkrecht, \( {\vec F}_{g\small N} \)​ (Abbildung 2-A).
Wir zeichnen die Kräfte in ein xy-Koordinatensystem ein (Abbildung 2-B).

Abb. 2

Lösung:

Anwendung des 2. Newtonschen Gesetzes

• x-Richtung:

die Hangabtriebskraft ist gegeben durch

die Gewichtskraft ist gegeben durch

Einsetzen der Gleichung (III) in die Gleichung (II)

Einsetzen der Gleichung (IV) in die Gleichung (I)

Das negative Vorzeichen der Beschleunigung zeigt an, dass sie in entgegengesetzter Richtung zur Orientierung der Bahn wirkt und der Block abgebremst wird.
Anwendung der Geschwindigkeitsgleichung als Funktion der zurückgelegten Strecke

Der Block wird verzögert, bis seine Endgeschwindigkeit null ist, v = 0. Durch Einsetzen der im Problem gegebenen Anfangsgeschwindigkeit sowie der oben berechneten Beschleunigung