Esercizio Risolto di Dinamica
pubblicità   

In una giornata senza vento, un’automobile si muove a velocità costante di 72 km/h. Il coefficiente di forma c è uguale a 0,6 unità SI (Sistema Internazionale di Unità di Misura) e l’area perpendicolare alla direzione del moto è di 3 m2. Determinare il modulo della forza di resistenza dell’aria.

 

Dati del problema:

  • Velocità dell’automobile:    v = 72 km/h;
  • Coefficiente di forma:    c = 0,6 S.I.;
  • Area della sezione trasversale:    A = 3 m2.

Schema del problema:

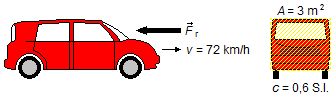
Nella Figura 1 sono mostrati gli elementi dati nel problema e la forza di resistenza dell’aria \( {\vec F}_r \) da calcolare.

Figura 1

Soluzione:

Innanzitutto, dobbiamo convertire la velocità dell’automobile data in chilometri orari (km/h) in metri al secondo (m/s) usati nel Sistema internazionale di unità di Misura (SI)

\[ \begin{gather} v=72\;\frac{\mathrm{\cancel{km}}}{\mathrm{\cancel h}}\times\frac{1000\;\mathrm m}{1\;\mathrm{\cancel{km}}}\times\frac{1\;\mathrm{\cancel h}}{3600\;\mathrm s}=\frac{72}{3,6}\;\frac{\mathrm m}{\mathrm s}=20\;\mathrm{m/s} \end{gather} \]

Il modulo della forza di resistenza dell’aria è dato da

\[ \begin{gather} \bbox[#99CCFF,10px] {F_r=Kv^2} \tag{I} \end{gather} \]

dove K è il coefficiente aerodinamico dato da

\[ \begin{gather} \bbox[#99CCFF,10px] {K=cA} \tag{II} \end{gather} \]

sostituendo l’equazione (II) nell’equazione (I)

\[ \begin{gather} F_r=cAv^2 \\[5pt] F_r=0,6\times 3\times 20^2 \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {F_r=720\;\mathrm N} \end{gather} \]
Osservazione: Il modulo della forza di resistenza è dato da
\[ \begin{gather} F_r=\frac{1}{2}c_r\mu Av^2 \end{gather} \]
dove cr è il coefficiente aerodinamico, μ la densità dell’aria, A l’area trasversale e v la velocità. Il coefficiente aerodinamico è una grandezza adimensionale.
In questo problema, il termine K è stato chiamato coefficiente aerodinamico, e dipende da un’altra costante c chiamata coefficiente di forma
\[ \begin{gather} F_r=\underbrace{\overbrace{\frac{1}{2}c_r\mu}^{c}A}_{K}v^2 \end{gather} \]
In questo caso, la costante K ha dimensione di massa per lunghezza,   \( \mathrm{M L^{-1}=\frac{kg}{m}} \)
pubblicità   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .