Gelöste Übung zur Dynamik

An einem windstillen Tag bewegt sich ein Auto mit konstanter Geschwindigkeit von 72 km/h. Der Formkonstante c beträgt 0,6 (SI-Einheiten), und die Querschnittsfläche senkrecht zur Bewegungsrichtung beträgt 3 m². Bestimmen Sie den Betrag der Luftwiderstandskraft.

Gegebene Daten:

Geschwindigkeit des Autos: v = 72 km/h;
Formkonstante: c = 0,6 SI;
Querschnittsfläche: A = 3 m².

Schema des Problems:

In Abbildung 1 sind die im Problem gegebenen Elemente sowie die zu berechnende Luftwiderstandskraft \( {\vec F}_r \) dargestellt.

Abb. 1

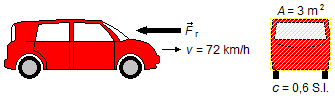
Lösung:

Zuerst müssen wir die im Problem angegebene Geschwindigkeit von Kilometern pro Stunde (km/h) in Meter pro Sekunde (m/s) umrechnen, wie es im Internationalen Einheitensystem (SI) üblich ist.

\[ \begin{gather} v=72\;\frac{\mathrm{\cancel{km}}}{\mathrm{\cancel h}}\times\frac{1000\;\mathrm m}{1\;\mathrm{\cancel{km}}}\times\frac{1\;\mathrm{\cancel h}}{3600\;\mathrm s}=\frac{72}{3,6}\;\frac{\mathrm m}{\mathrm s}=20\;\mathrm{m/s} \end{gather} \]

Der Betrag der Luftwiderstandskraft wird durch

\[ \begin{gather} \bbox[#99CCFF,10px] {F_r=Kv^2} \tag{I} \end{gather} \]

gegeben, wobei K der Widerstandsbeiwert ist, der durch

\[ \begin{gather} \bbox[#99CCFF,10px] {K=cA} \tag{II} \end{gather} \]

Einsetzen von Gleichung (II) in Gleichung (I)

\[ \begin{gather} F_r=cAv^2 \\[5pt] F_r=0,6\times 3\times 20^2 \end{gather} \]

\[ \begin{gather} \bbox[#FFCCCC,10px] {F_r=720\;\mathrm N} \end{gather} \]

Anmerkung: Der Betrag der Luftwiderstandskraft wird durch

\[ \begin{gather} F_r=\frac{1}{2}c_r\mu Av^2 \end{gather} \]

bestimmt, wobei c_r der Widerstandsbeiwert, μ die Luftdichte, A die Querschnittsfläche und v die Geschwindigkeit ist. Der aerodynamische Beiwert ist eine dimensionslose Größe.
In dieser Aufgabe wurde der Term K als Widerstandsbeiwert bezeichnet und hängt von einer weiteren Konstante c ab, dem sogenannten Formkonstante

\[ \begin{gather} F_r=\underbrace{\overbrace{\frac{1}{2}c_r\mu}^{c}A}_{K}v^2 \end{gather} \]

In diesem Fall hat die Konstante K die Dimension Masse pro Länge \( \mathrm{M L^{-1}=\frac{kg}{m}} \)

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .