Un treno ad alta velocità percorre una curva di 2500 m di raggio a una velocità di 270 km/h. Calcolare:
a) La forza centrifuga sentita da un passeggero, di massa pari a 70 kg, in un vagone di questo treno;
b) Quale dovrebbe essere la velocità di un’automobile, percorrendo una curva con 10 m di raggio, affinché quel passeggero del treno sentisse la stessa forza centrifuga trovandosi nell’automobile? Dare la risposta in km/h.

Dati del problema:

• Raggio della curva del treno:    r_T = 2500 m;
• Velocità del treno:    v_T = 270 km/h;
• Massa del passeggero:    m = 70 kg;
• Raggio della curva dell’automobile:    r_C = 10 m.

Schema del problema:

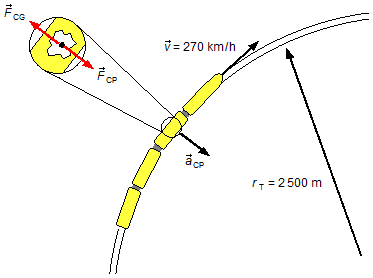
Quando il treno percorre la curva, agisce sul treno e sui corpi al suo interno (passeggeri e carichi) l’accelerazione centripeta, responsabile del moto curvilineo. Nel sistema di riferimento solidale con il treno i corpi sentono la forza centrifuga che equilibra la forza centripeta (Figura 1).

Figura 1

Soluzione:

Innanzitutto, dobbiamo convertire la velocità del treno data in chilometri orari (km/h) in metri al secondo (m/s) usati nel Sistema Internazionale di Unità di Misura (SI)

a) Applicando la Seconda Legge di Newton per il moto curvilineo

L’accelerazione centripeta è data da

Sostituendo l’equazione (II) nell’equazione (I)

Applicando l’equazione (III) al passeggero del treno

poiché la forza centripeta e la forza centrifuga devono essere uguali in modulo

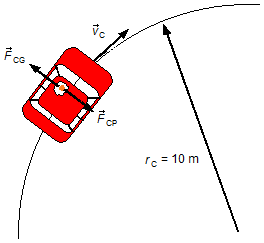
b) Se il passeggero del treno si trova in un’automobile, la forza centripeta (e la forza centrifuga) che agirà su di lui sarà, applicando l’equazione (III)

\[ \begin{gather} F_{cp}=F_{cg}=m\frac{v_{\small C}^2}{r_{\small C}} \\[5pt] v_{\small C}=\sqrt{{\frac{ F_{cg}r_{\small C} }{m}}\;} \\[5pt] v_{\small C}=\sqrt{\frac{157,5\times 10}{70}} \\[5pt] v_{\small C}=4,7\; \mathrm{m/s} \end{gather} \]

Figura 2

Convertendo la risposta in km/h