Ein Hochgeschwindigkeitszug fährt eine Kurve mit einem Radius von 2500 m mit einer Geschwindigkeit von 270 km/h. Berechnen Sie:
a) Die Zentrifugalkraft, die ein Fahrgast mit einer Masse von 70 kg in einem Waggon dieses Zuges verspürt;
b) Mit welcher Geschwindigkeit müsste ein Auto eine Kurve mit einem Radius von 10 m durchfahren, damit derselbe Fahrgast im Auto die gleiche Zentrifugalkraft wie im Zug verspürt? Geben Sie die Antwort in km/h an.

Gegebene Daten:

• Radius der Zugkurve: r_Z = 2500 m;
• Geschwindigkeit des Zuges: v_Z = 270 km/h;
• Masse des Fahrgastes: m = 70 kg;
• Radius der Autokurve: r_A = 10 m.

Schema des Problems:

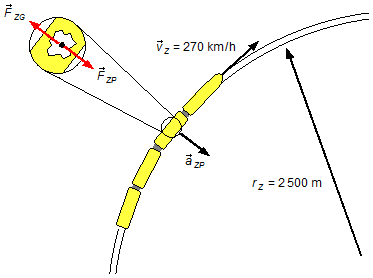
Wenn der Zug die Kurve fährt, wirkt auf den Zug und auf die sich darin befindenden Körper (Fahrgäste und Ladung) die Zentripetalbeschleunigung, die dafür verantwortlich ist, dass sich die Körper entlang der Kurve bewegen. Im Bezugssystem, das im Zug ruht, verspüren die Körper die Zentrifugalkraft, die die Zentripetalkraft ausgleicht (Abbildung 1).

Abb. 1

Lösung:

Zuerst müssen wir die Geschwindigkeit des Zuges von Kilometern pro Stunde (km/h) in Meter pro Sekunde (m/s) umrechnen, wie sie im Internationalen Einheitensystem (SI) verwendet werden

a) Anwendung des 2. Newtonschen Gesetzes auf eine gekrümmte Bahn

Die Zentripetalbeschleunigung ist gegeben durch

Einsetzen von Gleichung (II) in Gleichung (I)

Anwendung der Gleichung (III) auf den Fahrgast im Zug

da Zentripetalkraft und Zentrifugalkraft betragsmäßig gleich sein müssen

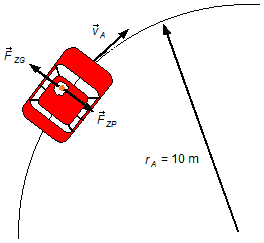
b) Befindet sich der Fahrgast aus dem Zug in einem Auto, so ergibt sich die auf ihn wirkende Zentripetalkraft (und damit auch die Zentrifugalkraft), wenn wir Gleichung (III) anwenden

\[ \begin{gather} F_{zp}=F_{zg}=m\frac{v_{\small A}^2}{r_{\small A}} \\[5pt] v_{\small A}=\sqrt{{\frac{ F_{zg}r_{\small A} }{m}}\;} \\[5pt] v_{\small A}=\sqrt{\frac{157,5\times 10}{70}} \\[5pt] v_{\small A}=4,7\; \mathrm{m/s} \end{gather} \]

Abb. 2

Umrechnung der Antwort in km/h