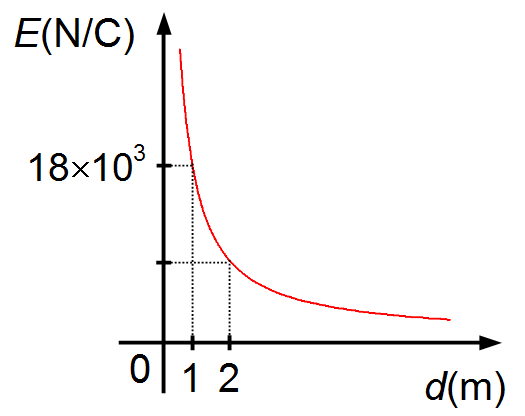
Le graphique représente la variation du champ électrique produit par une charge ponctuelle positive
Q en fonction de la distance jusqu'à la charge. La Constante de Coulomb dans le vide
est
\( k_e=9\times 10^9\;\mathrm{\frac{N.m^2}{C^2}} \).
Déterminer:
a) La valeur de la charge Q;
b) L'intensité de la force électrique agissant sur une charge
q = −1×10−5 C, placée à 2 m de Q;
c) L'intensité de la force électrique agissant sur une charge
q = 1×10−5 C, placée à 1 m de Q.
Données du problème:
- Charge électrique dans la situation 1: q1 = −1×10−5 C;
- Distance de la charge Q à la charge q1: d1 = 2 m;
- Charge électrique dans la situation 2: q2 = 1×10−5 C;
- Distance de la charge Q à la charge q2: d2 = 1 m;
-
Constante de Coulomb dans le vide:
\( k_e=9\times 10^9\;\mathrm{\frac{N.m^2}{C^2}} \).
Solution:
a) Le module du champ électrique est donné par
\[
\begin{gather}
\bbox[#99CCFF,10px]
{E=k_e\frac{q}{r^2}}
\end{gather}
\]
À partir du graphique, nous avons qu'à une distance r = 1 m de la charge Q, le champ
électrique est E = 18×103 N/C. En remplaçant ces données, nous trouvons la
charge Q.
\[
\begin{gather}
E=k_e\frac{Q}{r^2} \\[5pt]
Q=\frac{Er^2}{k_e} \\[5pt]
Q=\frac{18\times 10^3\times 1^2}{9\times 10^9} \\[5pt]
Q=2\times 10^3\times 10^{-9}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{Q=2\times 10^{-6}\;\mathrm C}
\end{gather}
\]
b) Selon la Loi de Coulomb, le module de la force électrique est donné par
\[
\begin{gather}
\bbox[#99CCFF,10px]
{F_{\small E}=k_e\frac{|\;q_1\;||\;q_2\;|}{r^2}} \tag{I}
\end{gather}
\]
en remplaçant la valeur de la charge trouvée dans l'article (a) et r = d1
\[
\begin{gather}
F_{\small E}=k_e\frac{|\;Q\;||\;q_{1}\;|}{d_{1}^{2}} \\[5pt]
F_{\small E}=9\times 10^9\times\frac{2\times 10^{-6}\times 1\times 10^{-5}}{2^2} \\[5pt]
F_{\small E}=4,5\times10^9\times 10^{-11}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{F_{\small E}=4,5\times 10^{-2}\;\mathrm N}
\end{gather}
\]
c) En appliquant à nouveau l'équation (I) et en remplaçant la valeur de la charge trouvée dans l'article
(a) et r = d2
\[
\begin{gather}
F_{\small E}=k_e\frac{|\;Q\;||\;q_{2}\;|}{d_{2}^{2}} \\[5pt]
F_{\small E}=9\times 10^9\times\frac{2\times 10^{-6}\times 1\times 10^{-5}}{1^2} \\[5pt]
F_{\small E}=18\times 10^9\times 10^{-11}
\end{gather}
\]
\[
\begin{gather}
\bbox[#FFCCCC,10px]
{F_{\small E}=18\times 10^{-2}\;\mathrm N}
\end{gather}
\]
Remarque: la charge 1 est négative, la force qui agit sur elle a la même direction et le sens
opposé au champ électrique. Dans le sens de la charge Q, les charges de signes opposés s'attirent.
La charge 2 est positive, la force qui agit sur elle a la même direction et le même sens que le champ
électrique, en sens opposé à la charge Q, les charges de signes identiques se repoussent.