Exercício Resolvido de Oscilações
publicidade
Determine a equação de movimento e o período de oscilações para um pêndulo físico, no regime de pequenas oscilações. O sistema consiste de um disco fino de massa m e raio a. O disco oscila em torno de um eixo colocado na borda do disco.
Dados do problema:
- Massa do disco: m;
- Raio do disco: a.
No pêndulo atua a seguintes força (Figura 1-A):
- P: força peso.
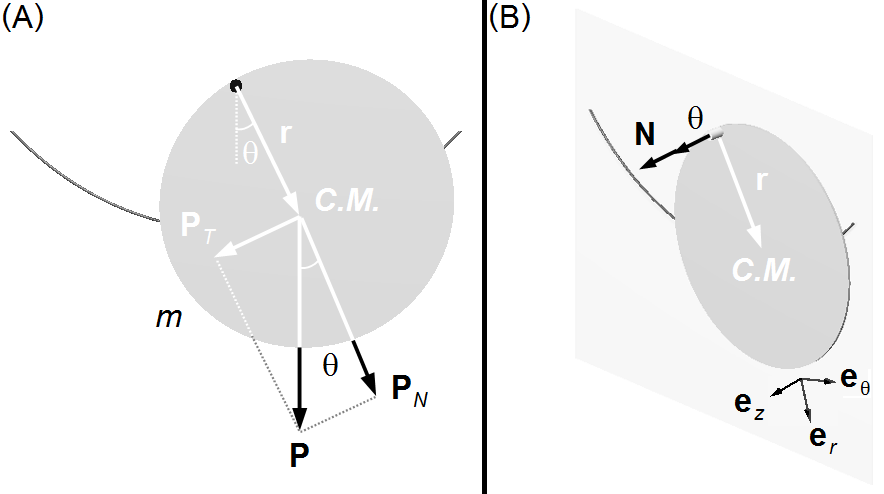
O vetor r localiza o Centro de Massa do disco que está a uma distância a igual ao raio em relação ao ponto de fixação.
Solução
Aplicando a 2.ª Lei de Newton para o movimento de rotação
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\mathbf{N}=I\mathbf{\alpha}} \tag{I}
\end{gather}
\]
- N é o torque da força que atua no corpo;
- I é o momento de inércia do corpo;
- α é a aceleração angular do corpo.
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\mathbf{N}=\mathbf{r}\times{\mathbf{F}}} \tag{II}
\end{gather}
\]
a única força que atua no corpo é a força peso P e |r| = a é a distância do ponto de
fixação até o Centro de Massa (C.M.) do pêndulo.Escrevendo a aceleração angular como
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\mathbf{\alpha}=\frac{d^{2}\mathbf{\theta}}{dt^{2}}} \tag{III}
\end{gather}
\]
substituindo as expressões (II) e (III) na expressão (I)
\[
\begin{gather}
\mathbf{r}\times{\mathbf{P}}=I\frac{d^{2}\mathbf{\theta}}{dt^{2}} \tag{IV}
\end{gather}
\]
onde
\( {\mathbf{P}}_{T}=-P\operatorname{sen}\theta\;{\mathbf{e}}_{\theta} \)
\( {\mathbf{P}}_{N}=P\cos \theta\;{\mathbf{e}}_{r} \)
\( \mathbf{r}=a\;{\mathbf{e}}_{r} \)
\( \mathbf{\theta}=\theta\;{\mathbf{e}}_{z} \)
Observação: Algumas pessoas acham dífícil entender que o vetor deslocamento angular aponte
na direção ez perpendicularmente ao plano de rotação. Quando um corpo se desloca
de uma posição r para uma posição r' temos um deslocamento s ao longo da trajetória,
o deslocamento angular θ está contido no plano, mas o vetor deslocamento angular θ
aponta perpendicularmente ao plano, isto preserva o produtor vetorial (Figura 2). O vetor deslocamento
angular indica que o corpo está em rotação, o seu módulo indica o deslocamento angular (escalar) e o
sentido do vetor indica o sentido de rotação do corpo, se o vetor θ é positivo o produto vetorial
indica que o corpo está se deslocando no sentido horário, se for negativo o corpo está se deslocando no
sentido anti-horário.
 Figura 2
Figura 2
Este é o mesmo argumento usado para a velocidade angular, o vetor velocidade v é tangente à trajetória, mas o vetor velocidade angular ω é perpendicular à trajetória.

Este é o mesmo argumento usado para a velocidade angular, o vetor velocidade v é tangente à trajetória, mas o vetor velocidade angular ω é perpendicular à trajetória.
\[
\begin{gather}
\mathbf{P}={\mathbf{P}}_{T}+{\mathbf{P}}_{N}\\
\mathbf{P}=-P\operatorname{sen}\theta\;{\mathbf{e}}_{\theta}+P\cos \theta\;{\mathbf{e}}_{r}
\end{gather}
\]
O produto vetorial
\( \mathbf{r}\times {\mathbf{P}} \)
será
\[
\begin{gather}
\mathbf{r}\times{\mathbf{P}}=
\left|
\begin{matrix}
{\mathbf{e}}_{r}& {\mathbf{e}}_{\theta} & {\mathbf{e}}_{z}\\
a & 0 & 0\\
P\cos \theta &-P\operatorname{sen}\theta & 0
\end{matrix}
\right|=\\[5pt]
=[0.0-0.(-P\operatorname{sen}\theta)]{\mathbf{e}}_{r}-[a.0-0.P\cos\theta]{\mathbf{e}}_{\theta}+[-aP\operatorname{sen}\theta-0.P\cos \theta]{\mathbf{e}}_{z}\\[5pt]
\mathbf{r}\times{\mathbf{P}}=-aP\operatorname{sen}\theta\;{\mathbf{e}}_{z} \tag{V}
\end{gather}
\]
a força peso é dada por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{P=mg} \tag{VI}
\end{gather}
\]
substituindo o valor de θ e as expressões (V) e (VI) na expressão (IV)
\[
\begin{gather}
-amg\operatorname{sen}\theta\;{\mathbf{e}}_{z}=I\frac{d^{2}\theta}{dt^{2}}\;{\mathbf{e}}_{z}\\[5pt]
\frac{-{amg}}{I}\operatorname{sen}\theta=\frac{d^{2}\theta}{dt^{2}}
\end{gather}
\]
a equação só possui componentes na direção ez, e fazendo a seguinte definição
\( \omega ^{2}=\frac{mga}{I} \)
e escrevendo
\( \frac{d^{2}\theta}{dt^{2}}=\ddot{\theta} \)
\[
\begin{gather}
\ddot{\theta}=-\omega ^{2}\operatorname{sen}\theta\\
\ddot{\theta}+\omega ^{2}\operatorname{sen}\theta =0
\end{gather}
\]
como estamos trabalhando em um regime de pequenas oscilações podemos expandir a função sen θ em uma
série de Taylor.
Expansão em série de Taylor de sen θ
\( \displaystyle \frac{f^{0}(0)}{0!}\theta ^{0}=\frac{\operatorname{sen}0}{1}.1=0 \)
Observação: \( f^{0} \) NÃO significa a função f elevada a potência zero, significa a derivada de ordem zero da função f, ou seja, a própria função calculada no pondo a.
\( \displaystyle \frac{f^{\text{I}}(0)}{1!}\theta ^{1}=\frac{\cos 0}{1}\theta =\theta \)
\( \displaystyle \frac{f^{\text{II}}(0)}{2!}\theta^{2}=\frac{-\operatorname{sen}0}{2.1}\theta ^{2}=0 \)
\( \displaystyle \frac{f^{\text{III}}(0)}{3!}\theta ^{3}=\frac{-\cos 0}{3.2.1}\theta^{3}=-{\frac{\theta ^{3}}{6}} \)
\( \displaystyle \frac{f^{\text{IV}}(0)}{4!}\theta^{4}=\frac{-(-\operatorname{sen}0)}{4.3.2.1}\theta ^{4}=0 \)
\( \displaystyle \frac{f^{\text{V}}(0)}{5!}\theta ^{5}=\frac{\cos 0}{5.4.3.2.1}\theta^{5}=\frac{\theta ^{5}}{120} \)
A função seno pode ser representada pela seguinte série de potências
Para um ângulo de \( 10°=\frac{\pi}{18}=0,1745 \), temos \( \operatorname{sen}\frac{\pi}{18}=0,1736 \), a aproximação representa um erro de 0,5%.
\[ \bbox[#99CCFF,10px]
{f(x)=\sum _{n=0}^{\infty}{\frac{f^{n}(a)}{n!}(x-a)^{n}}}
\]
fazendo a expansão em torno do ponto de equilíbrio com a = 0, para os 6 primeiros termos da série,
temos
\( \displaystyle \frac{f^{0}(0)}{0!}\theta ^{0}=\frac{\operatorname{sen}0}{1}.1=0 \)
Observação: \( f^{0} \) NÃO significa a função f elevada a potência zero, significa a derivada de ordem zero da função f, ou seja, a própria função calculada no pondo a.
\( \displaystyle \frac{f^{\text{I}}(0)}{1!}\theta ^{1}=\frac{\cos 0}{1}\theta =\theta \)
\( \displaystyle \frac{f^{\text{II}}(0)}{2!}\theta^{2}=\frac{-\operatorname{sen}0}{2.1}\theta ^{2}=0 \)
\( \displaystyle \frac{f^{\text{III}}(0)}{3!}\theta ^{3}=\frac{-\cos 0}{3.2.1}\theta^{3}=-{\frac{\theta ^{3}}{6}} \)
\[ \displaystyle \frac{f^{\text{III}}(0)}{3!}\theta ^{3}=\frac{-\cos 0}{3.2.1}\theta^{3}=-{\frac{\theta ^{3}}{6}} \]
\( \displaystyle \frac{f^{\text{IV}}(0)}{4!}\theta^{4}=\frac{-(-\operatorname{sen}0)}{4.3.2.1}\theta ^{4}=0 \)
\[ \displaystyle \frac{f^{\text{IV}}(0)}{4!}\theta^{4}=\frac{-(-\operatorname{sen}0)}{4.3.2.1}\theta ^{4}=0 \]
\( \displaystyle \frac{f^{\text{V}}(0)}{5!}\theta ^{5}=\frac{\cos 0}{5.4.3.2.1}\theta^{5}=\frac{\theta ^{5}}{120} \)
\[ \displaystyle \frac{f^{\text{V}}(0)}{5!}\theta ^{5}=\frac{\cos 0}{5.4.3.2.1}\theta^{5}=\frac{\theta ^{5}}{120} \]
A função seno pode ser representada pela seguinte série de potências
\[
\operatorname{sen}\theta =\theta -\frac{\theta ^{3}}{6}+\frac{\theta^{5}}{120}-...
\]
Como estamos considerando θ um ângulo pequeno podemos fazer a aproximação
\[
\operatorname{sen}\theta \approx \theta
\]
e desprezamos os termos de potências maiores.Para um ângulo de \( 10°=\frac{\pi}{18}=0,1745 \), temos \( \operatorname{sen}\frac{\pi}{18}=0,1736 \), a aproximação representa um erro de 0,5%.
\[
\ddot{\theta}+\omega ^{2}\theta =0
\]
Solução da equação diferencial \( \displaystyle \ddot{\theta}+\omega^{2}\theta =0 \)
A solução é do tipo exponencial, calculando suas derivadas
A solução é do tipo exponencial, calculando suas derivadas
\[
\begin{array}{l}
\theta =\operatorname{e}^{\lambda t} \\
\dot{\theta}=\lambda \operatorname{e}^{\lambda t} \\
\ddot{\theta}=\lambda^{2}\operatorname{e}^{\lambda t}
\end{array}
\]
substituindo na equação
\[
\begin{gather}
\lambda ^{2}\operatorname{e}^{\lambda t}+\omega^{2}\operatorname{e}^{\lambda t}=0\\[5pt]
\lambda^{2}+\omega^{2}=0\\[5pt]
\lambda ^{2}=-\omega^{2}\\[5pt]
\lambda =\pm i\sqrt{\omega^{2}}\\[5pt]
\lambda =\pm i\omega
\end{gather}
\]
a solução é da seguinte forma, onde C1 e C2 são constantes
\[
\theta (t)=C_{1}\operatorname{e}^{i\omega t}+C_{2}\operatorname{e}^{-i\omega t}
\]
usando a fórmula de Euler
\( \operatorname{e}^{ix}=\cos x+i\operatorname{sen}x \)
\[
\begin{gather}
\theta (t)=C_{1}\left(\cos \omega t+i\operatorname{sen}\omega t\right)+C_{2}\left(\cos \omega t-i\operatorname{sen}\omega t\right)\\[5pt]
\theta(t)=\left(C_{1}+C_{2}\right)\cos \omega t-i\left(C_{2}-C_{1}\right)\operatorname{sen}\omega t
\end{gather}
\]
definindo as seguintes constantes
\[
A=C_{1}+C_{2}\quad ,\quad B=i(C_{2}-C_{1})
\]
\[
\theta (t)=A\cos \omega t+B\operatorname{sen}\omega t
\]
fazendo as seguintes definições
\[
\begin{array}{l}
\cos \phi=\dfrac{A}{\sqrt{A^{2}+B^{2}}}\\[5pt]
\operatorname{sen}\phi=\dfrac{B}{\sqrt{A^{2}+B^{2}}}\\[5pt]
\theta_{0}=\sqrt{A^{2}+B^{2}}
\end{array}
\]
substituindo na equação
\[
\begin{gather}
\theta (t)=\left(A\cos \omega t-B\operatorname{sen}\omega t\right)\frac{\sqrt{A^{2}+B^{2}}}{\sqrt{A^{2}+B^{2}}}\\[5pt]
\theta(t)=\sqrt{A^{2}+B^{2}}\left(\frac{A}{\sqrt{A^{2}+B^{2}}}\cos \omega t-\frac{B}{\sqrt{A^{2}+B^{2}}}\operatorname{sen}\omega t\right)\\[5pt]
\theta (t)=\theta_{0}\left(\cos \phi \cos \omega t-\operatorname{sen}\phi \operatorname{sen}\omega t\right)
\end{gather}
\]
A equação de movimento será
\[ \bbox[#FFCCCC,10px]
{\theta (t)=\theta_{0}\cos \left(\omega t+\phi \right)}
\]
O período de oscilações é dado por
\[ \bbox[#99CCFF,10px]
{T=\frac{2\pi }{\omega}}
\]
substituindo a definição de ω0 feita acima
\[
\begin{gather}
T=\frac{2\pi }{\sqrt{\dfrac{mga}{I}}}\\[5pt]
{T=2\pi \sqrt{\frac{I}{mga}}} \tag{VII}
\end{gather}
\]
Calculando o momento de inércia de um disco de massa m com densidade constante σ, o momento de
inércia em relação a um eixo passando pelo Centro de Massa é dado por
\[
\begin{gather}
\bbox[#99CCFF,10px]
{I_{CM}=\int r^{2}\;dm} \tag{VIII}
\end{gather}
\]
Usando a expressão da densidade superficial de massa σ obtemos o elemento de massa dm
\[
\begin{gather}
\bbox[#99CCFF,10px]
{\sigma =\frac{dm}{dA}} \tag{IX}
\end{gather}
\]
\[
\begin{gather}
dm=\sigma \;dA \tag{IX}
\end{gather}
\]
onde dA é um elemento de área de ângulo dθ do disco (Figura 3)
\[
\begin{gather}
dA=r\;dr\;d\theta \tag{X}
\end{gather}
\]
substituindo a expressão (X) na expressão (IX)
\[
\begin{gather}
dm=\sigma r\;dr\;d\theta \tag{XI}
\end{gather}
\]
substituindo a expressão (XI) na expressão (VIII), e como a integração é feita sobre a superfície do
disco, depende de duas variáveis r e θ, temos uma integral dupla
\[
I_{CM}=\iint r^{2}\sigma r\;dr\;d\theta
\]
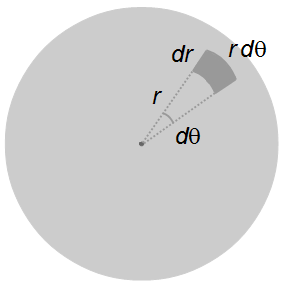
Figura 3
a densidade do disco é constante ela pode sair da integral
\[
I_{CM}=\sigma \iint r^{3}\;dr\;d\theta
\]
Os limites de integração serão de 0 até a em dr, ao longo do raio do disco, e de 0 até 2π
em dθ, uma volta completa no disco
\[
I_{CM}=\sigma \int_{0}^{a}r^{3}\;dr\int_{0}^{2\pi}\;d\theta
\]
Integral de \( \displaystyle \int_{0}^{{a}}r^{3}dr \)
\[
\int_{0}^{{a}}r^{3}dr=\left.\frac{r^{4}}{4}\;\right|_{\;0}^{\;a}=\frac{a^{4}}{4}-\frac{0^{4}}{4}=\frac{a^{4}}{4}
\]
Integral de \( \displaystyle \int_{0}^{{2\pi}}d\theta \)
\[
\int_{0}^{{2\pi}}d\theta =\left.\theta \;\right|_{\;0}^{\;2\pi}=2\pi-0=2\pi
\]
\[
\begin{gather}
I_{CM}=\sigma \frac{a^{4}}{4}2\pi\\
I_{CM}=\sigma a^{2}\pi \frac{a^{2}}{2}
\end{gather}
\]
o fator σa2π é a massa m total do disco (densidade superficial multiplicada pela área
do disco)
\[
\begin{gather}
I_{CM}=\frac{1}{2}ma^{2} \tag{XII}
\end{gather}
\]
Este é o momento de inércia do disco em relação ao eixo passando pelo Centro de Massa. O disco do
problema está oscilando em torno de um eixo na borda do disco a uma distância igual ao raio a do
disco (Figura 4). Pelo Teorema dos Eixos Paralelos
\[
\begin{gather}
\bbox[#99CCFF,10px]
{I_{p}=I_{CM}+md^{2}} \tag{XIII}
\end{gather}
\]
sendo d = a e substituindo a expressão (XII) na expressão (XIII)
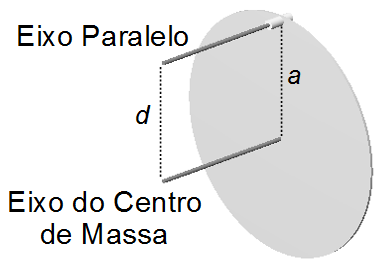
Figura 4
\[
\begin{gather}
I_{p}=\frac{1}{2}ma^{2}+ma^{2}\\
I_{p}=\frac{ma^{2}+2ma^{2}}{2}\\
I_{p}=\frac{3ma^{2}}{2} \tag{XIV}
\end{gather}
\]
substituindo a expressão (XIV) na expressão (VII)
\[
\begin{gather}
T=2\pi\sqrt{\frac{\dfrac{3ma^{2}}{2}}{mga}}\\[5pt]
T=2\pi\sqrt{\frac{3\cancel{m}a^{\cancel{2}}}{2\cancel{m}g\cancel{a}}}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{T=2\pi \sqrt{\frac{3a}{2g}}}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .