Exercício Resolvido de Oscilações Harmônicas
publicidade
Determine a equação de movimento e o período de oscilações para um pêndulo simples no regime de pequenas oscilações.
Esquema do problema:
Vamos adotar que o pêndulo é formado por uma esfera, de massa m, e uma corda de comprimento L, inextensível e de massa desprezível. Consideremos o raio da esfera muito pequeno, de tal modo que pode ser desprezado em relação ao comprimento da corda. Se a massa da corda e o raio da esfera não pudessem ser desprezados teríamos um pêndulo composto.
No pêndulo atuam as seguintes forças (Figura 1-A):
- P: força peso;
- T: força tração da corda.
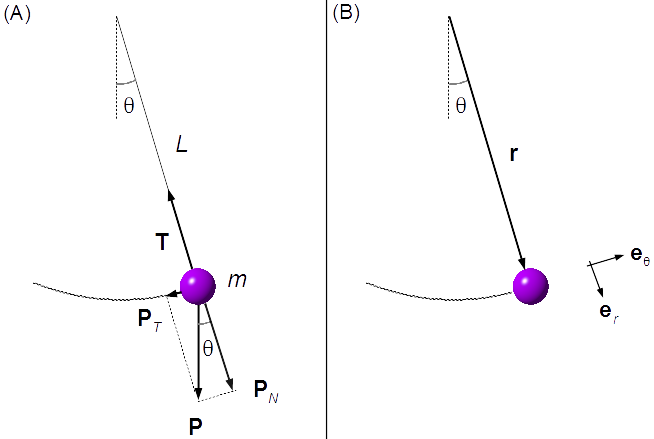
Adotamos um sistema de referência em coordenadas polares (Figura 1-B), onde er e eθ são os vetores unitários nas direções r e θ.
Solução
Aplicando a 2.ª. Lei de Newton ao pêndulo
\[ \bbox[#99CCFF,10px]
{\mathbf{F}=m\ddot{\mathbf{r}}}
\]
\[
\begin{gather}
\mathbf{P}-\mathbf{T}=m\ddot{\mathbf{r}}\\
{-\mathbf{P}}_{T}+{\mathbf{P}}_{N}+\mathbf{T}=m\ddot{\mathbf{r}}
\end{gather}
\]
onde
\( {\mathbf{P}}_{T}=P\operatorname{sen}\theta\;{\mathbf{e}}_{\theta} \)
\( {\mathbf{P}}_{N}=P\cos \theta\;{\mathbf{e}}_{r} \)
\( \mathbf{T}=T\;{\mathbf{e}}_{r} \)
e a aceleração em coordenadas polares é dada por
\[
\ddot{\mathbf{r}}=\left(\ddot{r}-r{\dot{\theta}}^{2}\right)\;{\mathbf{e}}_{r}+\left(r\ddot{\theta}+2\dot{r}\dot{\theta}\right)\;{\mathbf{e}}_{\theta}
\]
\[
-P\operatorname{sen}\theta \;{\mathbf{e}}_{\theta}+P\cos\theta\;{\mathbf{e}}_{r}-T\;{\mathbf{e}}_{r}=m\left[\left(\ddot{r}-r{\dot{\theta}}^{2}\right)\;{\mathbf{e}}_{r}+\left(r\ddot{\theta}+2\dot{r}\dot{\theta}\right)\;{\mathbf{e}}_{\theta}\right]
\]
Na direção er, a distância r representa o comprimento do fio L,
que é constante, o primeiro termo
(\( \ddot{r} \))
é nulo, derivada de uma constante é igual a zero, não há aceleração na direção radial.Na direção eθ, o segundo termo (\( 2\dot{r}\dot{\theta} \)) é igual a zero porque a derivada em r é nula pelo mesmo motivo anterior.
Separando as equações
\[
\begin{array}{l}
-mr{\dot{\theta}}^{2}\;{\mathbf{e}}_{r}=(P\cos \theta-T)\;{\mathbf{e}}_{r}\\
\phantom{()}mr\ddot{\theta}\;{\mathbf{e}}_{\theta}=-P\operatorname{sen}\theta\;{\mathbf{e}}_{\theta}
\end{array}
\]
fazendo r = L e substituindo a força peso
\[ \bbox[#99CCFF,10px]
{P=mg}
\]
\[
\begin{array}{l}
{\mathbf{e}}_{r}: \qquad -mL{\dot{\theta}}^{2}=mg\cos \theta-T\\[5pt]
{\mathbf{e}}_{\theta}: \qquad \phantom{-}\cancel{m}L\ddot{\theta}=-\cancel{m}g\operatorname{sen}\theta
\end{array}
\]
A segunda equação fornece a equação de movimento do pêndulo
\[
\begin{gather}
L\ddot{\theta}=-g\operatorname{sen}\theta\\[5pt]
\ddot{\theta}+\frac{g}{L}\operatorname{sen}\theta =0
\end{gather}
\]
como estamos trabalhando em um regime de pequenas oscilações podemos expandir a função sen θ em uma
série de Taylor.
Expansão em série de Taylor de sen θ
\( \displaystyle \frac{f^{0}(0)}{0!}\theta ^{0}=\frac{\operatorname{sen}0}{1}.1=0 \)
Observação: \( f^{0} \) NÃO significa a função f elevada a potência zero, significa a derivada de ordem zero da função f, ou seja, a própria função calculada no pondo a.
\( \displaystyle \frac{f^{\text{I}}(0)}{1!}\theta ^{1}=\frac{\cos 0}{1}\theta =\theta \)
\( \displaystyle \frac{f^{\text{II}}(0)}{2!}\theta^{2}=\frac{-\operatorname{sen}0}{2.1}\theta ^{2}=0 \)
\( \displaystyle \frac{f^{\text{III}}(0)}{3!}\theta ^{3}=\frac{-\cos 0}{3.2.1}\theta^{3}=-{\frac{\theta ^{3}}{6}} \)
\( \displaystyle \frac{f^{\text{IV}}(0)}{4!}\theta^{4}=\frac{-(-\operatorname{sen}0)}{4.3.2.1}\theta ^{4}=0 \)
\( \displaystyle \frac{f^{\text{V}}(0)}{5!}\theta ^{5}=\frac{\cos 0}{5.4.3.2.1}\theta^{5}=\frac{\theta ^{5}}{120} \)
A função seno pode ser representada pela seguinte série de potências
Para um ângulo de \( 10°=\frac{\pi}{18}=0,1745 \), temos \( \operatorname{sen}\frac{\pi}{18}=0,1736 \), a aproximação representa um erro de 0,5%.
\[ \bbox[#99CCFF,10px]
{f(x)=\sum _{n=0}^{\infty}{\frac{f^{n}(a)}{n!}(x-a)^{n}}}
\]
fazendo a expansão em torno do ponto de equilíbrio com a = 0, para os 6 primeiros termos da série,
temos
\( \displaystyle \frac{f^{0}(0)}{0!}\theta ^{0}=\frac{\operatorname{sen}0}{1}.1=0 \)
Observação: \( f^{0} \) NÃO significa a função f elevada a potência zero, significa a derivada de ordem zero da função f, ou seja, a própria função calculada no pondo a.
\( \displaystyle \frac{f^{\text{I}}(0)}{1!}\theta ^{1}=\frac{\cos 0}{1}\theta =\theta \)
\( \displaystyle \frac{f^{\text{II}}(0)}{2!}\theta^{2}=\frac{-\operatorname{sen}0}{2.1}\theta ^{2}=0 \)
\( \displaystyle \frac{f^{\text{III}}(0)}{3!}\theta ^{3}=\frac{-\cos 0}{3.2.1}\theta^{3}=-{\frac{\theta ^{3}}{6}} \)
\[ \displaystyle \frac{f^{\text{III}}(0)}{3!}\theta ^{3}=\frac{-\cos 0}{3.2.1}\theta^{3}=-{\frac{\theta ^{3}}{6}} \]
\( \displaystyle \frac{f^{\text{IV}}(0)}{4!}\theta^{4}=\frac{-(-\operatorname{sen}0)}{4.3.2.1}\theta ^{4}=0 \)
\[ \displaystyle \frac{f^{\text{IV}}(0)}{4!}\theta^{4}=\frac{-(-\operatorname{sen}0)}{4.3.2.1}\theta ^{4}=0 \]
\( \displaystyle \frac{f^{\text{V}}(0)}{5!}\theta ^{5}=\frac{\cos 0}{5.4.3.2.1}\theta^{5}=\frac{\theta ^{5}}{120} \)
\[ \displaystyle \frac{f^{\text{V}}(0)}{5!}\theta ^{5}=\frac{\cos 0}{5.4.3.2.1}\theta^{5}=\frac{\theta ^{5}}{120} \]
A função seno pode ser representada pela seguinte série de potências
\[
\operatorname{sen}\theta =\theta -\frac{\theta ^{3}}{6}+\frac{\theta^{5}}{120}-...
\]
Como estamos considerando θ um ângulo pequeno podemos fazer a aproximação
\[
\operatorname{sen}\theta \approx \theta
\]
e desprezamos os termos de potências maiores.Para um ângulo de \( 10°=\frac{\pi}{18}=0,1745 \), temos \( \operatorname{sen}\frac{\pi}{18}=0,1736 \), a aproximação representa um erro de 0,5%.
\[
\ddot{\theta}+\frac{g}{L}\theta =0
\]
Solução da equação diferencial \( \displaystyle \ddot{\theta}+\frac{g}{L}\theta =0 \)
A solução é do tipo exponencial, calculando suas derivadas
A solução é do tipo exponencial, calculando suas derivadas
\[
\begin{array}{l}
\theta =\operatorname{e}^{\lambda t} \\
\dot{\theta}=\lambda \operatorname{e}^{\lambda t} \\
\ddot{\theta}=\lambda^{2}\operatorname{e}^{\lambda t}
\end{array}
\]
substituindo na equação
\[
\begin{gather}
\lambda ^{2}\operatorname{e}^{\lambda t}+\frac{g}{L}\operatorname{e}^{\lambda t}=0\\[5pt]
\lambda^{2}+\frac{g}{L}=0\\[5pt]
\lambda ^{2}=-{\frac{g}{L}}\\[5pt]
\lambda =\pm i\sqrt{\frac{g}{L}}
\end{gather}
\]
fazendo a seguinte definição
\( \omega_{0}^{2}=\frac{g}{L} \)
a solução é da seguinte forma, onde C1 e C2 são constantes
\[
\theta (t)=C_{1}\operatorname{e}^{i\omega_{0}t}+C_{2}\operatorname{e}^{-i\omega_{0}t}
\]
usando a fórmula de Euler
\( \operatorname{e}^{ix}=\cos x+i\operatorname{sen}x \)
\[
\begin{gather}
\theta (t)=C_{1}\left(\cos \omega_{0}t+i\operatorname{sen}\omega_{0}t\right)+C_{2}\left(\cos \omega_{0}t-i\operatorname{sen}\omega_{0}t\right)\\[5pt]
\theta(t)=\left(C_{1}+C_{2}\right)\cos \omega_{0}t-i\left(C_{2}-C_{1}\right)\operatorname{sen}\omega_{0}t
\end{gather}
\]
definindo as seguintes constantes
\[
A=C_{1}+C_{2}\quad ,\quad B=i(C_{2}-C_{1})
\]
\[
\theta (t)=A\cos \omega_{0}t+B\operatorname{sen}\omega_{0}t
\]
fazendo as seguintes definições
\[
\begin{array}{l}
\cos \phi=\dfrac{A}{\sqrt{A^{2}+B^{2}}}\\[5pt]
\operatorname{sen}\phi=\dfrac{B}{\sqrt{A^{2}+B^{2}}}\\[5pt]
\theta_{0}=\sqrt{A^{2}+B^{2}}
\end{array}
\]
substituindo na equação
\[
\begin{gather}
\theta (t)=\left(A\cos \omega_{0}t-B\operatorname{sen}\omega_{0}t\right)\frac{\sqrt{A^{2}+B^{2}}}{\sqrt{A^{2}+B^{2}}}\\[5pt]
\theta(t)=\sqrt{A^{2}+B^{2}}\left(\frac{A}{\sqrt{A^{2}+B^{2}}}\cos \omega_{0}t-\frac{B}{\sqrt{A^{2}+B^{2}}}\operatorname{sen}\omega_{0}t\right)\\[5pt]
\theta (t)=\theta_{0}\left(\cos \phi \cos \omega_{0}t-\operatorname{sen}\phi \operatorname{sen}\omega_{0}t\right)
\end{gather}
\]
A equação de movimento será
\[ \bbox[#FFCCCC,10px]
{\theta (t)=\theta _{0}\cos \left(\omega_{0}t+\phi \right)}
\]
O período de oscilações é dado por
\[ \bbox[#99CCFF,10px]
{T=\frac{2\pi }{\omega_{0}}}
\]
substituindo a definição de ω0 feita acima
\[
T=\frac{2\pi }{\sqrt{\frac{g}{L}}}
\]
\[ \bbox[#FFCCCC,10px]
{T=2\pi \sqrt{\frac{L}{g}}}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .