Solved Problem on Harmonic Oscillations
advertisement
Determine the equation of motion as a function of time and the period of oscillations to a simple pendulum in the small oscillation approximation.
Problem diagram:
Let's assume that the pendulum consists of a sphere with a mass m swinging on a rope of length L, inextensible and with negligible mass. Consider the radius of the sphere small, so that it can be neglected relative to the length of the rope. If the mass of the rope and the radius of the sphere could not be neglected, we would have a compound pendulum.
On the pendulum acts the forces (Figure 1-A):
- Fg: gravitational force;
- T: tension force of the rope.
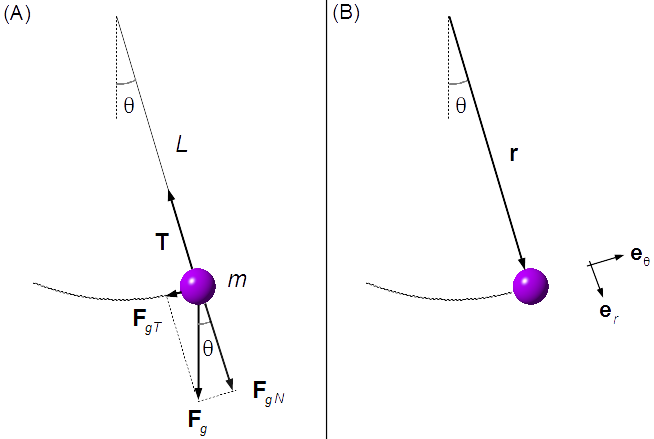
We choose a polar coordinate system (Figure 1-B), where er and eθ are the unit vectors in directions r and θ.
Solution
Applying Newton's Second Law to the pendulum
\[ \bbox[#99CCFF,10px]
{\mathbf{F}=m\ddot{\mathbf{r}}}
\]
\[
\begin{gather}
\mathbf{F}_{g}-\mathbf{T}=m\ddot{\mathbf{r}}\\
{-\mathbf{F}}_{gT}+{\mathbf{F}}_{gN}+\mathbf{T}=m\ddot{\mathbf{r}}
\end{gather}
\]
where
\( {\mathbf{F}}_{gT}=F_{g}\sin \theta\;{\mathbf{e}}_{\theta} \)
\( {\mathbf{F}}_{gN}=F_{g}\cos \theta\;{\mathbf{e}}_{r} \)
\( \mathbf{T}=T\;{\mathbf{e}}_{r} \)
and the acceleration in polar coordinates is given by
\[
\ddot{\mathbf{r}}=\left(\ddot{r}-r{\dot{\theta}}^{2}\right)\;{\mathbf{e}}_{r}+\left(r\ddot{\theta}+2\dot{r}\dot{\theta}\right)\;{\mathbf{e}}_{\theta}
\]
\[
-F_{g}\sin \theta \;{\mathbf{e}}_{\theta}+F_{g}\cos\theta\;{\mathbf{e}}_{r}-T\;{\mathbf{e}}_{r}=m\left[\left(\ddot{r}-r{\dot{\theta}}^{2}\right)\;{\mathbf{e}}_{r}+\left(r\ddot{\theta}+2\dot{r}\dot{\theta}\right)\;{\mathbf{e}}_{\theta}\right]
\]
In the direction er, the distance r represents the length of the string
L, which is constant, the first term
(\( \ddot{r} \))
is null, the derivative of a constant is equal to zero, and there is no acceleration in the radial direction.In the direction eθ, the second term (\( 2\dot{r}\dot{\theta} \)) is zero because the derivative in r is null for the same reason.
Separating the equations
\[
\begin{array}{l}
-mr{\dot{\theta}}^{2}\;{\mathbf{e}}_{r}=(F_{g}\cos \theta-T)\;{\mathbf{e}}_{r}\\
\phantom{()}mr\ddot{\theta}\;{\mathbf{e}}_{\theta}=-F_{g}\sin \theta\;{\mathbf{e}}_{\theta}
\end{array}
\]
lets r = L and substitute the gravitational force
\[ \bbox[#99CCFF,10px]
{F_{g}=mg}
\]
\[
\begin{array}{l}
{\mathbf{e}}_{r}: \qquad -mL{\dot{\theta}}^{2}=mg\cos \theta-T\\[5pt]
{\mathbf{e}}_{\theta}: \qquad \phantom{-}\cancel{m}L\ddot{\theta}=-\cancel{m}g\sin \theta
\end{array}
\]
The second equation gives the equation of motion of the pendulum
\[
\begin{gather}
L\ddot{\theta}=-g\sin \theta\\[5pt]
\ddot{\theta}+\frac{g}{L}\sin \theta =0
\end{gather}
\]
as we are working on a small angle approximation oscillations, we can expand the sin θ function in a
Taylor series.
Taylor series expansion of sin θ
\( \displaystyle \frac{f^{0}(0)}{0!}\theta ^{0}=\frac{\sin 0}{1}.1=0 \)
Note: \( f^{0} \) DOES NOT mean the function f to the zero power means the zero derivatives of the function f, that is, the function itself calculated in the point a.
\( \displaystyle \frac{f^{\text{I}}(0)}{1!}\theta ^{1}=\frac{\cos 0}{1}\theta =\theta \)
\( \displaystyle \frac{f^{\text{II}}(0)}{2!}\theta^{2}=\frac{-\sin 0}{2.1}\theta ^{2}=0 \)
\( \displaystyle \frac{f^{\text{III}}(0)}{3!}\theta ^{3}=\frac{-\cos 0}{3.2.1}\theta^{3}=-{\frac{\theta ^{3}}{6}} \)
\( \displaystyle \frac{f^{\text{IV}}(0)}{4!}\theta^{4}=\frac{-(-\sin 0)}{4.3.2.1}\theta ^{4}=0 \)
\( \displaystyle \frac{f^{\text{V}}(0)}{5!}\theta ^{5}=\frac{\cos 0}{5.4.3.2.1}\theta^{5}=\frac{\theta ^{5}}{120} \)
The sine function can be represented by the following series of powers
For an angle of \( 10°=\frac{\pi}{18}=0,1745 \), we have \( \sin \frac{\pi}{18}=0,1736 \), the approach represents an error of 0.5%.
\[ \bbox[#99CCFF,10px]
{f(x)=\sum _{n=0}^{\infty}{\frac{f^{n}(a)}{n!}(x-a)^{n}}}
\]
expanding around the equilibrium point with a = 0, for the first 6 terms of the series, we have
\( \displaystyle \frac{f^{0}(0)}{0!}\theta ^{0}=\frac{\sin 0}{1}.1=0 \)
Note: \( f^{0} \) DOES NOT mean the function f to the zero power means the zero derivatives of the function f, that is, the function itself calculated in the point a.
\( \displaystyle \frac{f^{\text{I}}(0)}{1!}\theta ^{1}=\frac{\cos 0}{1}\theta =\theta \)
\( \displaystyle \frac{f^{\text{II}}(0)}{2!}\theta^{2}=\frac{-\sin 0}{2.1}\theta ^{2}=0 \)
\( \displaystyle \frac{f^{\text{III}}(0)}{3!}\theta ^{3}=\frac{-\cos 0}{3.2.1}\theta^{3}=-{\frac{\theta ^{3}}{6}} \)
\[ \displaystyle \frac{f^{\text{III}}(0)}{3!}\theta ^{3}=\frac{-\cos 0}{3.2.1}\theta^{3}=-{\frac{\theta ^{3}}{6}} \]
\( \displaystyle \frac{f^{\text{IV}}(0)}{4!}\theta^{4}=\frac{-(-\sin 0)}{4.3.2.1}\theta ^{4}=0 \)
\[ \displaystyle \frac{f^{\text{IV}}(0)}{4!}\theta^{4}=\frac{-(-\sin 0)}{4.3.2.1}\theta ^{4}=0 \]
\( \displaystyle \frac{f^{\text{V}}(0)}{5!}\theta ^{5}=\frac{\cos 0}{5.4.3.2.1}\theta^{5}=\frac{\theta ^{5}}{120} \)
\[ \displaystyle \frac{f^{\text{V}}(0)}{5!}\theta ^{5}=\frac{\cos 0}{5.4.3.2.1}\theta^{5}=\frac{\theta ^{5}}{120} \]
The sine function can be represented by the following series of powers
\[
\sin \theta =\theta -\frac{\theta ^{3}}{6}+\frac{\theta^{5}}{120}-...
\]
As we are considering θ a small angle, we can make the approach
\[
\sin \theta \approx \theta
\]
and we neglect higher-order terms.For an angle of \( 10°=\frac{\pi}{18}=0,1745 \), we have \( \sin \frac{\pi}{18}=0,1736 \), the approach represents an error of 0.5%.
\[
\ddot{\theta}+\frac{g}{L}\theta =0
\]
Solution of the differential equation \( \displaystyle \ddot{\theta}+\frac{g}{L}\theta =0 \)
The solution is exponential type, calculating its derivatives
The solution is exponential type, calculating its derivatives
\[
\begin{array}{l}
\theta =\operatorname{e}^{\lambda t} \\
\dot{\theta}=\lambda \operatorname{e}^{\lambda t} \\
\ddot{\theta}=\lambda^{2}\operatorname{e}^{\lambda t}
\end{array}
\]
substituting in the equation
\[
\begin{gather}
\lambda ^{2}\operatorname{e}^{\lambda t}+\frac{g}{L}\operatorname{e}^{\lambda t}=0\\[5pt]
\lambda^{2}+\frac{g}{L}=0\\[5pt]
\lambda ^{2}=-{\frac{g}{L}}\\[5pt]
\lambda =\pm i\sqrt{\frac{g}{L}}
\end{gather}
\]
setting
\( \omega_{0}^{2}=\frac{g}{L} \)
the solution is as follows, where C1 and C2 are constant
\[
\theta (t)=C_{1}\operatorname{e}^{i\omega_{0}t}+C_{2}\operatorname{e}^{-i\omega_{0}t}
\]
using Euler's formula
\( \operatorname{e}^{ix}=\cos x+i\sin x \)
\[
\begin{gather}
\theta (t)=C_{1}\left(\cos \omega_{0}t+i\sin \omega_{0}t\right)+C_{2}\left(\cos \omega_{0}t-i\sin \omega_{0}t\right)\\[5pt]
\theta(t)=\left(C_{1}+C_{2}\right)\cos \omega_{0}t-i\left(C_{2}-C_{1}\right)\sin \omega_{0}t
\end{gather}
\]
defining the following constants
\[
A=C_{1}+C_{2}\quad ,\quad B=i(C_{2}-C_{1})
\]
\[
\theta (t)=A\cos \omega_{0}t+B\sin \omega_{0}t
\]
setting
\[
\begin{array}{l}
\cos \phi=\dfrac{A}{\sqrt{A^{2}+B^{2}}}\\[5pt]
\sin \phi=\dfrac{B}{\sqrt{A^{2}+B^{2}}}\\[5pt]
\theta_{0}=\sqrt{A^{2}+B^{2}}
\end{array}
\]
substituting in the equation
\[
\begin{gather}
\theta (t)=\left(A\cos \omega_{0}t-B\sin \omega_{0}t\right)\frac{\sqrt{A^{2}+B^{2}}}{\sqrt{A^{2}+B^{2}}}\\[5pt]
\theta(t)=\sqrt{A^{2}+B^{2}}\left(\frac{A}{\sqrt{A^{2}+B^{2}}}\cos \omega_{0}t-\frac{B}{\sqrt{A^{2}+B^{2}}}\sin \omega_{0}t\right)\\[5pt]
\theta (t)=\theta_{0}\left(\cos \phi \cos \omega_{0}t-\sin \phi \sin\omega_{0}t\right)
\end{gather}
\]
The equation of motion will be
\[ \bbox[#FFCCCC,10px]
{\theta (t)=\theta _{0}\cos \left(\omega_{0}t+\phi \right)}
\]
The period of oscillations is given by
\[ \bbox[#99CCFF,10px]
{T=\frac{2\pi }{\omega_{0}}}
\]
substituting the definition of ω0 made above
\[
T=\frac{2\pi }{\sqrt{\frac{g}{L}}}
\]
\[ \bbox[#FFCCCC,10px]
{T=2\pi \sqrt{\frac{L}{g}}}
\]
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .