Exercício Resolvido de Dinâmica
publicidade
No sistema da figura são conhecidas as massas m1 e m2. Calcule o
ângulo θ e as tensões nas cordas para que o sistema permaneça em equilíbrio. Despreze a massa da
roldana e os atritos.
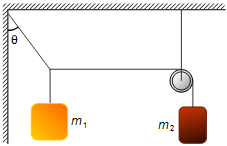
Dados do problema:
- Massa do bloco 1: m1;
- Massa do bloco 2: m2.
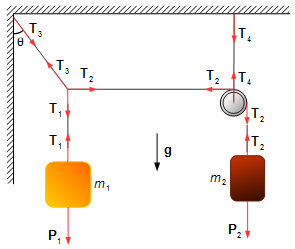
Isolamos os corpos e pesquisamos as forças em cada um deles.
Adotamos um sistema de referência com o vetor unitário j com sentido positivo para baixo.
Bloco 1:
- P1: força peso do bloco 1;
- T1: tração da corda.
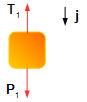
Figura 2
Bloco 2:
- P2: força peso do bloco 2;
- T2: tração da corda.
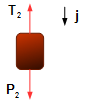
Figura 3
Ponto de contato das trações T1, T2 e T4:
- T1: tração na corda devido ao bloco 1;
- T2: tração na corda devido ao bloco 2;
- T3: tração na corda devido à fixação na parede.
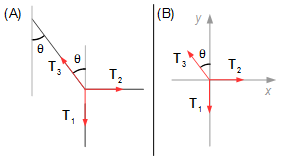
A corda forma um ângulo θ com a parede, traçando uma linha vertical que passa pelo ponto de encontro dos três vetores, o ângulo entre o vetor T3 e a vertical também será θ, são ângulos alternos internos (Figura 4).
Polia:
- T4: tração na corda que fixa a polia no teto.
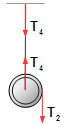
Figura 5
Para que o sistema permaneça em equilíbrio temos a condição de que a somatória das forças que atuam sobre ele é zero
\[ \bbox[#99CCFF,10px]
{\sum {\mathbf{F}}=0}
\]
Bloco 1:
\[
{\mathbf{P}}_{1}+{\mathbf{T}}_{1}=0
\]
onde
\( {\mathbf{T}}_{1}=-T_{1}\;\mathbf{j} \)
\( {\mathbf{P}}_{1}=m_{1}g\;\mathbf{j} \)
\[
m_{1}g\;\mathbf{j}-T_{1}\;\mathbf{j}=0
\]
Só existem componentes na direção j
\[ \bbox[#FFCCCC,10px]
{T_{1}=m_{1}g}
\]
Bloco 2:
\[
{\mathbf{P}}_{2}+{\mathbf{T}}_{2}=0
\]
onde
\( {\mathbf{T}}_{2}=-T_{2}\;\mathbf{j} \)
\( {\mathbf{P}}_{2}=m_{2}g\;\mathbf{j} \)
\[
m_{2}g\;\mathbf{j}-T_{2}\;\mathbf{j}=0
\]
Só existem componentes na direção j
\[ \bbox[#FFCCCC,10px]
{T_{2}=m_{2}g}
\]
Ponto de contato das trações T1, T2 e T3:
\[
{\mathbf{T}}_{1}+{\mathbf{T}}_{2}+{\mathbf{T}}_{3}=0
\]
onde i e j são o vetores unitários nas direções x e y
\( {\mathbf{T}}_{1}=-m_{1}g\;\mathbf{j} \)
\( {\mathbf{T}}_{2}=m_{2}g\;\mathbf{i} \)
\( {\mathbf{T}}_{3}=-T_{3}\operatorname{sen}\theta\;\mathbf{i}+T_{3}\cos \theta\;\mathbf{j} \)
\[
-m_{1}g\;\mathbf{j}+m_{2}g\;\mathbf{i}-T_{3}\operatorname{sen}\theta\;\mathbf{i}+T_{3}\cos \theta\;\mathbf{j}=0
\]
Separando as componentes
\[
\begin{gather}
\left\{
\begin{matrix}
\begin{aligned}
m_{2}g-T_{3}\operatorname{sen}\theta=0\\
-m_{1}g+T_{3}\cos \theta=0
\end{aligned}
\end{matrix}\right.\\[10pt]
\left\{
\begin{matrix}
T_{3}\operatorname{sen}\theta=m_{2}g\\
T_{3}\cos \theta=m_{1}g
\end{matrix}\right.
\end{gather}
\]
dividindo a primeira equação pela segunda
\[
\begin{gather}
\frac{T_{3}\operatorname{sen}\theta}{T_{3}\cos \theta}=\frac{m_{2}g}{m_{1}g}\\[5pt]
\frac{\operatorname{sen}\theta}{\cos \theta}=\frac{m_{2}}{m_{1}}\\[5pt]
\operatorname{tg}\theta=\frac{m_{2}}{m_{1}}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{\theta=\operatorname{arctg}\left(\frac{m_{2}}{m_{1}}\right)}
\]
Para encontrarmos T3 substituímos esse ângulo na primeira equação do sistema
\[
T_{3}\operatorname{sen}\left[\operatorname{arctg}\left(\frac{m_{2}}{m_{1}}\right)\right]=m_{2}g
\]
Lembrando das relações trigonométricas
\[
\operatorname{sen}\left(\operatorname{arctg}x\right)=\frac{x}{\sqrt{x^{2}+1}}
\]
\[
\begin{gather}
T_{3}\left(\frac{\dfrac{m_{2}}{m_{1}}}{\sqrt{\left(\dfrac{m_{2}}{m_{1}}\right)^{2}+1}}\right)=m_{2}g\\[5pt]
T_{3}\frac{m_{2}}{m_{1}\sqrt{\left(\dfrac{m_{2}}{m_{1}}\right)^{2}+1}}=m_{2}g
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{T_{3}=m_{1}g\sqrt{\left(\frac{m_{2}}{m_{1}}\right)^{2}+1}}
\]
Polia:
Como a polia não possui massa e atrito ela apenas transfere as trações aplicadas nas cordas. A tração T2, devido ao bloco 2, é transferida para o ponto de encontro das trações T1 e T3 (Figura 1), e da polia para o teto (Figura 5)
\[
T_{4}=T_{2}
\]
\[ \bbox[#FFCCCC,10px]
{T_{4}=m_{2}g}
\]
Observação: A relação trigonométrica
\( \operatorname{sen}\left(\operatorname{arctg}x\right)=\frac{x}{\sqrt{x^{2}+1}} \)
é obtida tomando-se um triângulo retângulo de hipotenusa a e catetos b e c
com ângulo θ (Figura 6).
\[
\begin{gather}
\operatorname{tg}\theta=\frac{b}{c} \tag{I}
\end{gather}
\]
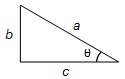
Figura 6
\[
\begin{gather}
\operatorname{tg}\theta=\operatorname{tg}\left(\operatorname{arctg}x\right)=x=\frac{x}{1} \tag{II}
\end{gather}
\]
igualando as expressões (I) e (II)
\[
\frac{b}{c}=\frac{x}{1}
\]
assim determinamos os catetos b e c
\[
\begin{gather}
b=x\\[10pt]
c=1
\end{gather}
\]
A hipotenusa é encontrada usando o Teorema de Pitágoras
\[
\begin{gather}
a^{2}=b^{2}+c^{2}\\
a^{2}=x^{2}+1^{2}\\
a=\sqrt{x^{2}+1^{2}\;}
\end{gather}
\]
O seno do ângulo θ será
\[
\operatorname{sen}\theta=\frac{x}{\sqrt{x^{2}+1\;}}
\]
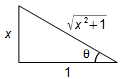
Figura 7
Da expressão (II)
\[
\theta=\operatorname{arctg}x
\]
Portanto
\[
\operatorname{sen}\left(\operatorname{arctg}x\right)=\frac{x}{\sqrt{x^{2}+1}}
\]
publicidade

Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .