Solved Problem on Dynamics
advertisement
In the system, the masses m1 and m2 are known. Find the angle θ and
the tension forces on the ropes so that the system remains in equilibrium. The pulley is lightweight
and frictionless.
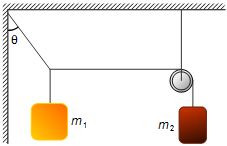
Problem data:
- Mass of block 1: m1;
- Mass of block 2: m2.
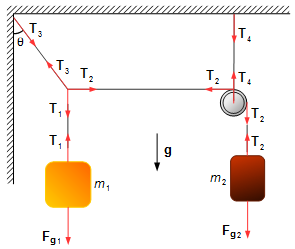
We draw free-bodies diagrams and we have the forces in each of them.
We choose a reference frame with the unit vector j pointing downward.
Block 1:
- Fg1: gravitational force on block 1;
- T1: tension force.
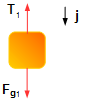
Figure 2
Block 2:
- Fg2: gravitational force on block 2;
- T2: tension force.
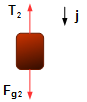
Figure 3
Point of contact of tension forces T1, T2, and T4:
- T1: tension force due to block 1;
- T2: tension force due to block 2;
- T3: tension force due to the fixed point on the wall.
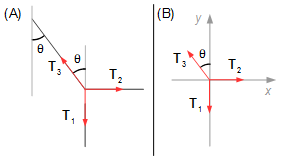
The rope makes an angle θ with the wall, drawing a vertical line that passes through the point of the three vectors, the angle between the vector T3 and the vertical will also be θ, they are alternate angles (Figure 4).
Pulley:
- T4: tension force on the rope that fixes the pulley on the ceiling.
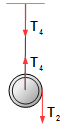
Figure 5
For the system to be in static equilibrium, we have the condition that the sum of the forces acting on it is zero
\[ \bbox[#99CCFF,10px]
{\sum {\mathbf{F}}=0}
\]
Block 1:
\[
{\mathbf{F}}_{g1}+{\mathbf{T}}_{1}=0
\]
where
\( {\mathbf{T}}_{1}=-T_{1}\;\mathbf{j} \)
\( {\mathbf{F}}_{g1}=m_{1}g\;\mathbf{j} \)
\[
m_{1}g\;\mathbf{j}-T_{1}\;\mathbf{j}=0
\]
There are only components in the direction j
\[ \bbox[#FFCCCC,10px]
{T_{1}=m_{1}g}
\]
Block 2:
\[
{\mathbf{F}}_{g2}+{\mathbf{T}}_{2}=0
\]
where
\( {\mathbf{T}}_{2}=-T_{2}\;\mathbf{j} \)
\( {\mathbf{F}}_{g2}=m_{2}g\;\mathbf{j} \)
\[
m_{2}g\;\mathbf{j}-T_{2}\;\mathbf{j}=0
\]
There are only components in the direction j
\[ \bbox[#FFCCCC,10px]
{T_{2}=m_{2}g}
\]
Contact point of tension forces T1, T2, and T3:
\[
{\mathbf{T}}_{1}+{\mathbf{T}}_{2}+{\mathbf{T}}_{3}=0
\]
where i and j are the unit vectors in directions x and y
\( {\mathbf{T}}_{1}=-m_{1}g\;\mathbf{j} \)
\( {\mathbf{T}}_{2}=m_{2}g\;\mathbf{i} \)
\( {\mathbf{T}}_{3}=-T_{3}\sin \theta\;\mathbf{i}+T_{3}\cos \theta\;\mathbf{j} \)
\[
-m_{1}g\;\mathbf{j}+m_{2}g\;\mathbf{i}-T_{3}\sin \theta\;\mathbf{i}+T_{3}\cos \theta\;\mathbf{j}=0
\]
Separating the components
\[
\begin{gather}
\left\{
\begin{matrix}
\begin{aligned}
m_{2}g-T_{3}\sin \theta=0\\
-m_{1}g+T_{3}\cos \theta=0
\end{aligned}
\end{matrix}\right.\\[10pt]
\left\{
\begin{matrix}
T_{3}\sin \theta=m_{2}g\\
T_{3}\cos \theta=m_{1}g
\end{matrix}\right.
\end{gather}
\]
dividing the first equation by the second
\[
\begin{gather}
\frac{T_{3}\sin \theta}{T_{3}\cos \theta}=\frac{m_{2}g}{m_{1}g}\\[5pt]
\frac{\sin \theta}{\cos \theta}=\frac{m_{2}}{m_{1}}\\[5pt]
\tan \theta=\frac{m_{2}}{m_{1}}
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{\theta=\arctan \left(\frac{m_{2}}{m_{1}}\right)}
\]
To find T3 we substitute this angle in the first system equation
\[
T_{3}\sin \left[\arctan \left(\frac{m_{2}}{m_{1}}\right)\right]=m_{2}g
\]
From the trigonometric identities
\[
\sin \left(\arctan x\right)=\frac{x}{\sqrt{x^{2}+1}}
\]
\[
\begin{gather}
T_{3}\left(\frac{\dfrac{m_{2}}{m_{1}}}{\sqrt{\left(\dfrac{m_{2}}{m_{1}}\right)^{2}+1}}\right)=m_{2}g\\[5pt]
T_{3}\frac{m_{2}}{m_{1}\sqrt{\left(\dfrac{m_{2}}{m_{1}}\right)^{2}+1}}=m_{2}g
\end{gather}
\]
\[ \bbox[#FFCCCC,10px]
{T_{3}=m_{1}g\sqrt{\left(\frac{m_{2}}{m_{1}}\right)^{2}+1}}
\]
Pulley:
Since the pulley has no mass and friction it only transfers the applied tension to the ropes. The tension T2, due to block 2, is transferred to the attaching point of tensions T1 and T3 (Figure 1), and from the pulley to the ceiling (Figure 5)
\[
T_{4}=T_{2}
\]
\[ \bbox[#FFCCCC,10px]
{T_{4}=m_{2}g}
\]
Note: The trigonometric identity
\( \sin \left(\arctan x\right)=\frac{x}{\sqrt{x^{2}+1}} \)
is obtained by taking from a right triangle with hypotenuse a and legs b and c
with angle θ (Figure 6).
\[
\begin{gather}
\tan \theta=\frac{b}{c} \tag{I}
\end{gather}
\]
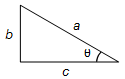
Figure 6
\[
\begin{gather}
\tan \theta=\tan\left(\arctan x\right)=x=\frac{x}{1} \tag{II}
\end{gather}
\]
equating the expressions (I) and (II)
\[
\frac{b}{c}=\frac{x}{1}
\]
thus we determine the b and c legs
\[
\begin{gather}
b=x\\[10pt]
c=1
\end{gather}
\]
The hypotenuse is found using the Pythagorean Theorem
\[
\begin{gather}
a^{2}=b^{2}+c^{2}\\
a^{2}=x^{2}+1^{2}\\
a=\sqrt{x^{2}+1^{2}\;}
\end{gather}
\]
The sine from angle θ will be
\[
\sin \theta=\frac{x}{\sqrt{x^{2}+1\;}}
\]
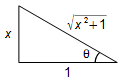
Figure 7
From the expression (II)
\[
\theta=\arctan x
\]
Therefore
\[
\sin \left(\arctan x\right)=\frac{x}{\sqrt{x^{2}+1}}
\]
advertisement

Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .