Exercício Resolvido de Transmissão de Calor
publicidade   



Uma parede constitui-se de duas chapas sobrepostas, feitas de diferentes materiais. Os coeficientes de condutibilidade térmica e as espessuras das chapas são iguais k1, d1 e k2, d2 respectivamente. As temperaturas das superfícies externas das paredes são iguais a T1 e T2 (T1 > T2) e mantêm-se constantes. Determinar:
a) A temperatura na superfície de interface entre as duas chapas;
b) Se as espessuras das duas chapas forem iguais, qual o coeficiente de condutibilidade térmica da parede.


Dados do problema:
  • Coeficiente de condutibilidade térmica da chapa 1:    k1;
  • Espessura da chapa 1:    d1;
  • Temperatura externa da chapa 1:    T1;
  • Coeficiente de condutibilidade térmica da chapa 2:    k2;
  • Espessura da chapa 2:    d2;
  • Temperatura externa da chapa 2:    T2.
Solução

a) O fluxo de calor é dado por
\[ \bbox[#99CCFF,10px] {\phi =kA\frac{\left(t_{1}-t_{2}\right)}{e}} \]
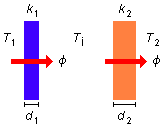
O calor passa do meio de maior temperatura T1 para o meio de menor temperatura T2, sendo Ti a temperatura na interface das duas chapas e A a área delas, o fluxo através da chapa 1 é dado por
\[ \begin{gather} \phi_{1}=k_{1}A\frac{\left(T_{1}-T_{i}\right)}{d_{1}} \tag{I} \end{gather} \]
o fluxo através da chapa 2 é dado por
\[ \begin{gather} \phi_{2}=k_{2}A\frac{\left(T_{i}-T_{2}\right)}{d_{2}} \tag{II} \end{gather} \]
Como as superfícies são mantidas às temperaturas constantes o fluxo de calor está em regime estacionário (Figura 1), os fluxos através das duas superfícies devem ser iguais
\[ \begin{gather} \phi _{1}=\phi_{2}\\[5pt] k_{1}\cancel{A}\frac{\left(T_{1}-T_{i}\right)}{d_{1}}=k_{2}\cancel{A}\frac{\left(T_{i}-T_{2}\right)}{d_{2}}\\[5pt] k_{1}\frac{\left(T_{1}-T_{i}\right)}{d_{1}}=k_{2}\frac{\left(T_{i}-T_{2}\right)}{d_{2}} \end{gather} \]
Figura 1

multiplicando em “cruz”
\[ \begin{gather} k_{1}d_{2}\left(T_{1}-T_{i}\right)=k_{2}d_{1}\left(T_{i}-T_{2}\right)\\[5pt] k_{1}d_{2}T_{1}-k_{1}d_{2}T_{i}=k_{2}d_{1}T_{i}-k_{2}d_{1}T_{2}\\[5pt] k_{2}d_{1}T_{i}+k_{1}d_{2}T_{i}=k_{1}d_{2}T_{1}+k_{2}d_{1}T_{2}\\[5pt] T_{i}\left(k_{2}d_{1}+k_{1}d_{2}\right)=k_{1}d_{2}T_{1}+k_{2}d_{1}T_{2} \end{gather} \]
\[ \bbox[#FFCCCC,10px] {T_{i}=\frac{k_{1}d_{2}T_{1}+k_{2}d_{1}T_{2}}{k_{2}d_{1}+k_{1}d_{2}}} \]

b) Para espessuras iguais (d1 = d2 = d) a expressão obtida no item anterior para a temperatura na interface se reduz a
\[ T_{i}=\frac{k_{1}dT_{1}+k_{2}dT_{2}}{k_{2}d+k_{1}d} \]
colocando a espessura d em evidência no numerador e no denominador
\[ \begin{gather} T_{i}=\frac{\cancel{d}\left(k_{1}T_{1}+k_{2}T_{2}\right)}{\cancel{d}\left(k_{2}+k_{1}\right)}\\[5pt] T_{i}=\frac{k_{1}T_{1}+k_{2}T_{2}}{k_{2}+k_{1}} \tag{III} \end{gather} \]
substituindo a expressão (III) na expressão (I) e d1 = d
\[ \phi_{1}=k_{1}A\frac{\left(T_{1}-\dfrac{k_{1}T_{1}+k_{2}T_{2}}{k_{2}+k_{1}}\right)}{d} \]
colocando os termos entre parênteses sobre o mesmo denominador (k2+k1)
\[ \begin{gather} \phi_{1}=k_{1}A\frac{\left(\dfrac{T_{1}\left(k_{2}+k_{1}\right)-k_{1}T_{1}-k_{2}T_{2}}{k_{2}+k_{1}}\right)}{d}\\[5pt][5pt] \phi_{1}=k_{1}\frac{A}{d}\left(\frac{k_{2}T_{1}+k_{1}T_{1}-k_{1}T_{1}-k_{2}T_{2}}{k_{2}+k_{1}}\right)\\[5pt][5pt] \phi_{1}=k_{1}\frac{A}{d}\left(\frac{k_{2}T_{1}-k_{2}T_{2}}{k_{2}+k_{1}}\right) \end{gather} \]
colocando o termo   \( \dfrac{k_{2}}{k_{2}+k_{1}} \)   em evidência
\[ \begin{gather} \phi_{1}=\frac{k_{1}k_{2}}{k_{1}+k_{2}}\frac{A}{d}\left(T_{1}-T_{2}\right) \tag{IV} \end{gather} \]
A espessura total será de 2d e sendo k o coeficiente de condutibilidade térmica do conjunto, o fluxo de calor através da parede como um todo pode ser escrito como (Figura 2)
\[ \begin{gather} \phi =kA\frac{\left(T_{1}-T_{2}\right)}{2d} \tag{V} \end{gather} \]

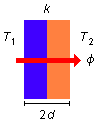
Figura 2

Como o regime de fluxo é estacionário as expressões (IV) e (V) devem ser iguais
\[ \begin{gather} \phi =\phi_{1}\\[5pt] k\frac{A}{2d}\left(T_{1}-T_{2}\right)=\frac{k_{1}k_{2}}{k_{1}+k_{2}}\frac{A}{d}\left(T_{1}-T_{2}\right)\\[5pt] \frac{k}{2}=\frac{k_{1}k_{2}}{k_{1}+k_{2}} \end{gather} \]
\[ \bbox[#FFCCCC,10px] {k=\frac{2k_{1}k_{2}}{k_{1}+k_{2}}} \]

Observação: Poderíamos substituir a expressão (III) na expressão (II)
\[ \phi_{2}=k_{2}A\frac{\left(\dfrac{k_{1}T_{1}+k_{2}T_{2}}{k_{2}+k_{1}}-T_{2}\right)}{d} \]
colocando os termos entre parênteses no mesmo denominador (k2+k1)
\[ \begin{gather} \phi_{2}=k_{2}A\frac{\left(\dfrac{k_{1}T_{1}+k_{2}T_{2}-T_{2}\left(k_{2}+k_{1}\right)}{k_{2}+k_{1}}\right)}{d}\\[5pt] \phi_{2}=k_{2}\frac{A}{d}\left(\frac{k_{1}T_{1}+k_{2}T_{2}-k_{1}T_{2}-k_{1}T_{2}}{k_{2}+k_{1}}\right)\\[5pt] \phi_{2}=k_{2}\frac{A}{d}\left(\frac{k_{1}T_{1}-k_{1}T_{2}}{k_{2}+k_{1}}\right) \end{gather} \]
colocando o termo \( \dfrac{k_{1}}{k_{2}+k_{1}} \) em evidência
\[ \phi_{2}=\frac{k_{1}k_{2}}{k_{1}+k_{2}}\frac{A}{d}\left(T_{1}-T_{2}\right) \]
Este resultado é equivalente à expressão (IV) encontrada acima.
publicidade   

Licença Creative Commons
Fisicaexe - Exercícios Resolvidos de Física de Elcio Brandani Mondadori está licenciado com uma Licença Creative Commons - Atribuição-NãoComercial-Compartilha Igual 4.0 Internacional .