Solved Problem on Heat Transfer
advertisement   



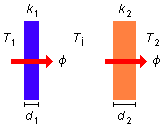
A wall consists of two overlapping sheets made of different materials. The heat transfer coefficients and the sheet thicknesses are equal to k1, d1 and k2, d2, respectively. The temperatures of the external surfaces of the walls are equal to T1 and T2 (T1 > T2) and remain constant. Determine:
a) The temperature at the interface between the two plates;
b) If the thicknesses of the two sheets are the same, what is the heat transfer coefficient of the wall.


Problem data:
  • Heat transfer coefficient of sheet 1:    k1;
  • Thickness of plate 1:    d1;
  • External temperature of plate 1:    T1;
  • Heat transfer coefficient of sheet 2:    k2;
  • Thickness of plate 2:    d2;
  • External temperature of plate 2:    T2.
Solution

a) The heat flux is given by
\[ \bbox[#99CCFF,10px] {\phi =kA\frac{\left(t_{1}-t_{2}\right)}{e}} \]
Heat passes from the higher temperature medium T1 to the lower temperature medium T2, where Ti is the temperature at the interface of the two plates and A is their area, the flux through plate 1 is given by
\[ \begin{gather} \phi_{1}=k_{1}A\frac{\left(T_{1}-T_{i}\right)}{d_{1}} \tag{I} \end{gather} \]
the flux through plate 2 is given by
\[ \begin{gather} \phi_{2}=k_{2}A\frac{\left(T_{i}-T_{2}\right)}{d_{2}} \tag{II} \end{gather} \]
Since the surfaces are kept at constant temperatures and the heat flux is steady (Figure 1), the fluxes through the two surfaces must be equal.
\[ \begin{gather} \phi _{1}=\phi_{2}\\[5pt] k_{1}\cancel{A}\frac{\left(T_{1}-T_{i}\right)}{d_{1}}=k_{2}\cancel{A}\frac{\left(T_{i}-T_{2}\right)}{d_{2}}\\[5pt] k_{1}\frac{\left(T_{1}-T_{i}\right)}{d_{1}}=k_{2}\frac{\left(T_{i}-T_{2}\right)}{d_{2}} \end{gather} \]
Figure 1

cross multiplying
\[ \begin{gather} k_{1}d_{2}\left(T_{1}-T_{i}\right)=k_{2}d_{1}\left(T_{i}-T_{2}\right)\\[5pt] k_{1}d_{2}T_{1}-k_{1}d_{2}T_{i}=k_{2}d_{1}T_{i}-k_{2}d_{1}T_{2}\\[5pt] k_{2}d_{1}T_{i}+k_{1}d_{2}T_{i}=k_{1}d_{2}T_{1}+k_{2}d_{1}T_{2}\\[5pt] T_{i}\left(k_{2}d_{1}+k_{1}d_{2}\right)=k_{1}d_{2}T_{1}+k_{2}d_{1}T_{2} \end{gather} \]
\[ \bbox[#FFCCCC,10px] {T_{i}=\frac{k_{1}d_{2}T_{1}+k_{2}d_{1}T_{2}}{k_{2}d_{1}+k_{1}d_{2}}} \]

b) For equal thicknesses (d1 = d2 = d) the expression obtained in the previous item for the temperature at the interface reduces to
\[ T_{i}=\frac{k_{1}dT_{1}+k_{2}dT_{2}}{k_{2}d+k_{1}d} \]
factoring the thickness d n the numerator and denominator
\[ \begin{gather} T_{i}=\frac{\cancel{d}\left(k_{1}T_{1}+k_{2}T_{2}\right)}{\cancel{d}\left(k_{2}+k_{1}\right)}\\[5pt] T_{i}=\frac{k_{1}T_{1}+k_{2}T_{2}}{k_{2}+k_{1}} \tag{III} \end{gather} \]
substituting expression (III) into expression (I) and d1 = d
\[ \phi_{1}=k_{1}A\frac{\left(T_{1}-\dfrac{k_{1}T_{1}+k_{2}T_{2}}{k_{2}+k_{1}}\right)}{d} \]
writing the terms in parentheses over the same denominator (k2+k1)
\[ \begin{gather} \phi_{1}=k_{1}A\frac{\left(\dfrac{T_{1}\left(k_{2}+k_{1}\right)-k_{1}T_{1}-k_{2}T_{2}}{k_{2}+k_{1}}\right)}{d}\\[5pt][5pt] \phi_{1}=k_{1}\frac{A}{d}\left(\frac{k_{2}T_{1}+k_{1}T_{1}-k_{1}T_{1}-k_{2}T_{2}}{k_{2}+k_{1}}\right)\\[5pt][5pt] \phi_{1}=k_{1}\frac{A}{d}\left(\frac{k_{2}T_{1}-k_{2}T_{2}}{k_{2}+k_{1}}\right) \end{gather} \]
factoring the term   \( \dfrac{k_{2}}{k_{2}+k_{1}} \)
\[ \begin{gather} \phi_{1}=\frac{k_{1}k_{2}}{k_{1}+k_{2}}\frac{A}{d}\left(T_{1}-T_{2}\right) \tag{IV} \end{gather} \]
The total thickness will be 2d and k heat transfer coefficient of the assembly, the heat flux through the wall as a whole can be written as (Figure 2)
\[ \begin{gather} \phi =kA\frac{\left(T_{1}-T_{2}\right)}{2d} \tag{V} \end{gather} \]

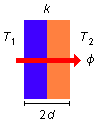
Figura 2

As the flow is in a steady state, expressions (IV) and (V) must be equal.
\[ \begin{gather} \phi =\phi_{1}\\[5pt] k\frac{A}{2d}\left(T_{1}-T_{2}\right)=\frac{k_{1}k_{2}}{k_{1}+k_{2}}\frac{A}{d}\left(T_{1}-T_{2}\right)\\[5pt] \frac{k}{2}=\frac{k_{1}k_{2}}{k_{1}+k_{2}} \end{gather} \]
\[ \bbox[#FFCCCC,10px] {k=\frac{2k_{1}k_{2}}{k_{1}+k_{2}}} \]

Note: We could substitute expression (III) into expression (II)
\[ \phi_{2}=k_{2}A\frac{\left(\dfrac{k_{1}T_{1}+k_{2}T_{2}}{k_{2}+k_{1}}-T_{2}\right)}{d} \]
writing the terms in parentheses over the same denominator (k2+k1)
\[ \begin{gather} \phi_{2}=k_{2}A\frac{\left(\dfrac{k_{1}T_{1}+k_{2}T_{2}-T_{2}\left(k_{2}+k_{1}\right)}{k_{2}+k_{1}}\right)}{d}\\[5pt] \phi_{2}=k_{2}\frac{A}{d}\left(\frac{k_{1}T_{1}+k_{2}T_{2}-k_{1}T_{2}-k_{1}T_{2}}{k_{2}+k_{1}}\right)\\[5pt] \phi_{2}=k_{2}\frac{A}{d}\left(\frac{k_{1}T_{1}-k_{1}T_{2}}{k_{2}+k_{1}}\right) \end{gather} \]
factoring the term   \( \dfrac{k_{1}}{k_{2}+k_{1}} \)
\[ \phi_{2}=\frac{k_{1}k_{2}}{k_{1}+k_{2}}\frac{A}{d}\left(T_{1}-T_{2}\right) \]
This result is equivalent to the expression (IV) found above.
advertisement   

Creative Commons License
Fisicaexe - Physics Solved Problems by Elcio Brandani Mondadori is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License .