Exercício Resolvido de Estática
publicidade

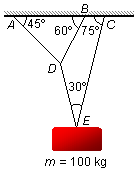
Um bloco de massa m=100 kg está suspenso pelo sistema de cordas mostrada na figura. Determinar as forças de tensão em todas as cordas.
Dados: \( \operatorname{sen}15°=0,259 \), \( \cos 15°=0,966 \), \( \operatorname{sen}45°=0,707 \), \( \cos 45°=0,707 \), \( \operatorname{sen}60°=0,866 \), \( \cos 60°=0,5 \).

Dados do problema:

  • Massa do bloco: m=100 kg;
  • Aceleração da gravidade: g=9,8 m/s2.

Esquema do problema:

Desenhando as forças que atuam no sistema.
No bloco a força peso \( \vec P \) é equilibrada pela força de tensão \( {\vec T}_1 \), que tem como força de reação \( {\vec T}\text{'}_1 \) no teto, e pela força de tensão \( {\vec T}_2 \), que tem como força de reação \( {\vec T}\text{'}_2 \) que está aplicada no ponto D.
No ponto D a força de tensão \( {\vec T}\text{'}_2 \) é equilibrada pelas forças de tensão \( {\vec T}_3 \) e \( {\vec T}_4 \), que tem como forças de reação \( {\vec T}\text{'}_3 \) e \( {\vec T}\text{'}_4 \) no teto.
Figura 1

Solução:

Como o sistema está em equilíbrio a resultante das forças é nula e aplicamos a condição

\[ \begin{gather} \bbox[#99CCFF,10px] {\sum F=0} \tag{I} \end{gather} \]

Dividindo o problema em duas partes, primeiro estudando as forças no bloco.
Pelo ponto C traçamos uma reta vertical perpendicular ao teto, o ângulo entre o teto e a corda \( \overline{CE} \) é de 75°, então o ângulo entre a reta traçada e a corda \( \overline{CE} \) é de 15°, são ângulos complementares, somam 90° (Figura 2-A).
A partir do bloco no ponto E traçamos uma reta vertical dividindo o ângulo de 30° em duas partes. Como o ângulo entre esta reta e a corda \( \overline{CE} \) é alterno interno com o ângulo encontrado anteriormente, ele também medirá 15°. Esta reta divide o ângulo de 30° em duas partes iguais, é uma bissetriz do ângulo de 30°.

Figura 2

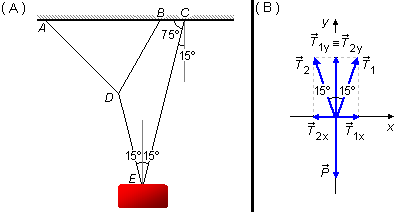
Desenhando as forças que atuam no bloco (Figura 2-B) em um sistema de coordenadas xy e decompondo as forças. A força peso \( \vec P \) só tem componente na direção y, as forças de tensão \( {\vec T}_1 \) e \( {\vec T}_2 \) têm componentes \( {\vec T}_{1x} \) e \( {\vec T}_{2x} \) na direção x e componentes \( {\vec T}_{1y} \) e \( {\vec T}_{2y} \) na direção y.

\[ \begin{gather} {\vec T}_1+{\vec T}_2+\vec P=0 \\[5pt] {\vec T}_{1x}+{\vec T}_{1y}-{\vec T}_{2x}+{\vec T}_{2y}-\vec P=0 \tag{II} \end{gather} \]
  • Direção x:
\[ \begin{gather} T_{1x}=T_1\operatorname{sen}15° \tag{III} \\[10pt] T_{2x}=T_2\operatorname{sen}15° \tag{IV} \end{gather} \]
Observação: ao contrário do que se faz usualmente em que o ângulo é medido em relação ao eixo-x e a componente nessa direção é proporcional ao cosseno, o ângulo foi medido em relação ao eixo-y e a componente é proporcional ao seno do ângulo.
  • Direção y:
\[ \begin{gather} T_{1y}=T_1\cos 15° \tag{V} \\[10pt] T_{2y}=T_2\cos 15° \tag{VI} \end{gather} \]

A força peso é dada por

\[ \begin{gather} \bbox[#99CCFF,10px] {P=mg} \tag{VII} \end{gather} \]

Substituindo as equações (III), (IV), (V), (VI) e (VII) na equação (II) e separando as componentes nas direções x e y.

  • Direção x:
\[ \begin{gather} T_1\operatorname{sen}15°-T_2\operatorname{sen}15°=0 \end{gather} \]
  • Direção y:
\[ \begin{gather} T_1\cos 15°+T_2\cos 15°-mg=0 \end{gather} \]

estas equações formam um sistema de duas equações a duas incógnitas (T1 e T2)

\[ \begin{gather} \left\{ \begin{array}{l} T_1\operatorname{sen}15°-T_2\operatorname{sen}15°=0\\ T_1\cos 15°+T_2\cos 15°-P=0 \end{array} \right. \end{gather} \]

isolando T1 na primeira equação do sistema

\[ \begin{gather} T_1\operatorname{sen}15°-T_2\operatorname{sen}15°=0 \\[5pt] T_1\cancel{\operatorname{sen}15°}=T_2\cancel{\operatorname{sen}15°} \\[5pt] T_1=T_2 \tag{VIII} \end{gather} \]

substituindo o valor de (VIII) na segunda equação do sistema

\[ \begin{gather} T_2\cos 15°+T_2\cos 15°-mg=0 \\[5pt] 2 T_2\cos 15°=mg \\[5pt] T_2=\frac{mg}{2\cos 15°} \end{gather} \]

substituindo os dados do problema

\[ \begin{gather} T_2=\frac{100\times 9,8}{2\times 0,966} \\[5pt] T_2=507,3 \end{gather} \]

pela igualdade (VII)

\[ \begin{gather} \bbox[#FFCCCC,10px] {T_1=T_2=507,3\;\mathrm N} \end{gather} \]

Estudando as forças que atuam no ponto D.
Traçando uma linha horizontal pelo ponto D, o ângulo entre esta reta e a corda \( \overline{AD} \) mede 45º, é um ângulo alterno interno com ângulo entre a corda \( \overline{AD} \) e o teto (Figura 3-A).
O ângulo entre a corda \( \overline{BD} \) e a reta horizontal mede 60º, é um ângulo alterno interno com o ângulo entre a corda \( \overline{BD} \) e o teto.
Traçando uma reta vertical pelo ponto D o ângulo entre a corda \( \overline{DE} \) e esta linha é de 15º, é alterno interno com o ângulo encontrado na primeira parte do problema.

Figura 3

Desenhando as forças no ponto D (Figura 3-B) em um sistema de coordenadas xy e decompondo as forças, a força de tensão \( {\vec T}_2 \) já foi determinada, têm as componentes \( {\vec T}_{2x} \) e \( {\vec T}_{2y} \). As forças de tensão \( {\vec T}_3 \) e \( {\vec T}_4 \) têm componentes \( {\vec T}_{3x} \) e \( {\vec T}_{4x} \) na direção x e componentes \( {\vec T}_{3y} \) e \( {\vec T}_{4y} \) na direção y.
Como o sistema está equilíbrio podemos aplicar a condição (I)

\[ \begin{gather} {\vec T}_2+{\vec T}_3+{\vec T}_4=0 \\[5pt] {\vec T}_{2x}-{\vec T}_{2y}+{\vec T}_{3x}+{\vec T}_{3y}-{\vec T}_{4x}+{\vec T}_{4y}=0 \tag{IX} \end{gather} \]
  • Direção x:
\[ \begin{gather} T_{2x}=T_2\operatorname{sen}15° \tag{X} \\[10pt] T_{3x}=T_3\cos 60° \tag{XI} \\[10pt] T_{4x}=T_4\cos 45° \tag{XII} \end{gather} \]
  • Direção y:
\[ \begin{gather} T_{2y}=T_2\cos 15° \tag{XIII} \\[10pt] T_{3y}=T_3\operatorname{sen}60° \tag{XIV} \\[10pt] T_{4y}=T_4\operatorname{sen}45° \tag{XV} \end{gather} \]

Substituindo as equações (X), (XI), (XII), (XIII), (XIV) e (XV) na equação (IX) e separando as componentes nas direções x e y.

  • Direção x:
\[ \begin{gather} T_2\operatorname{sen}15°+T_3\cos 60°-T_4\cos 45°=0\\[5pt] \end{gather} \]
  • Direção y:
\[ \begin{gather} T_3\operatorname{sen}60°+T_4\operatorname{sen}45°-T_2\cos 15°=0 \end{gather} \]

estas equações formam um sistema de duas equações a duas incógnitas (T3 e T4)

Observação: T2 não é uma incógnita, já foi determinado anteriormente, então passamos os termos em T2 nas duas equações para o lado direito da igualdade.
\[ \begin{gather} &\left\{ \begin{matrix} T_2\operatorname{sen}15°+T_3\cos 60°-T_4\cos 45°=0\\ T_3\operatorname{sen}60°+T_4\operatorname{sen}45°-T_2\cos 15°=0 \end{matrix} \right.\\[8pt] &\left\{ \begin{matrix} T_3\cos 60°-T_4\cos 45°=-T_2\operatorname{sen}15°\\ T_3\operatorname{sen}60°+T_4\operatorname{sen}45°=T_2\cos 15° \end{matrix} \right. \end{gather} \]

somando as duas equações do sistema eliminamos o termo em T4

\[ \begin{gather} \frac{ \begin{matrix} T_3\cos 60°-\cancel{T_4\cos 45°}=-T_2\operatorname{sen}15°\\ T_3\operatorname{sen}60°+\cancel{T_4\operatorname{sen}45°}=T_2\cos 15° \end{matrix}} {T_3(\cos 60°+\operatorname{sen}60°)+0=T_2(\cos 15°-\operatorname{sen}15°)}\\[5pt] T_3=\frac{\cos 15°-\operatorname{sen}15°}{\cos 60°+\operatorname{sen}60°}\,T_2 \end{gather} \]
Observação: lembre-se que cos 45° é igual a sen 45°, então esses termos se cancelam quando somamos as duas equações, eles têm sinais opostos nas equações.

substituindo os valores dados no problema e a tensão T2 determinada acima

\[ \begin{gather} T_3=\frac{0,966-0,258}{0,500+0,866}\times 507,3 \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {T_3=262,9\;\mathrm N} \end{gather} \]

Isolando T4 na segunda equação do sistema

\[ \begin{gather} T_3\operatorname{sen}60°+T_4\operatorname{sen}45°=T_2\cos 15° \\[5pt] T_4=\frac{T_2\cos 15°-T_3\operatorname{sen}60°}{\operatorname{sen}45°} \end{gather} \]

substituindo os valores dados no problema e as tensões T2 e T3 determinadas acima

\[ \begin{gather} T_4=\frac{507,3\times 0,966-262,9\times 0,866}{0,707} \end{gather} \]
\[ \begin{gather} \bbox[#FFCCCC,10px] {T_4=371,1\;\mathrm N} \end{gather} \]
publicidade